非线性谐振子的方程为:
我们假设加入非线性项之后,依然是一个周期函数,但振动的周期和函数形式不再是简单的简谐振动。但由于它还是周期函数(假设这个原频率为),我们可以对它进行傅里叶级数展开:
其中是各项的振幅。
微扰法求解非线性谐振子 {.title1}
问题简述
非线性谐振子的方程为:
x¨+ω02x+Ax2+Bx3+⋯=0
我们假设加入非线性项之后,x(t)依然是一个周期函数,但振动的周期和函数形式不再是简单的简谐振动sin(ω0t),cos(ω0t)。但由于它还是周期函数(假设这个原频率为ω),我们可以对它进行傅里叶级数展开:
x(t)=n=−∞∑∞fneinωt
其中fn是各项的振幅。
xn的计算
我们有了x(t)的展开式,如何计算各阶非线性项中xn(t)的值?这是计算的核心问题
x(t)x2(t)=n=−∞∑∞fneinωt=n=−∞∑∞m−∞∑∞fnfmei(n+m)ωt=u=−∞∑∞(n=−∞∑∞fnfu−n)eiuωt=u=−∞∑∞gueiuωt
其中gu=(f∗f)u=∑n=−∞∞fnfu−n是序列fn和自己的离散卷积
同理,xk(t)的计算就是k个序列fn作离散卷积,结果与fn一样,也构成一个无穷序列。下面我们展示一个离散卷积的计算示例。
离散卷积
我们将以f(0)为例,展示卷积的计算过程。f(0)的表达式为:
f1(0)=af−1(0)=a
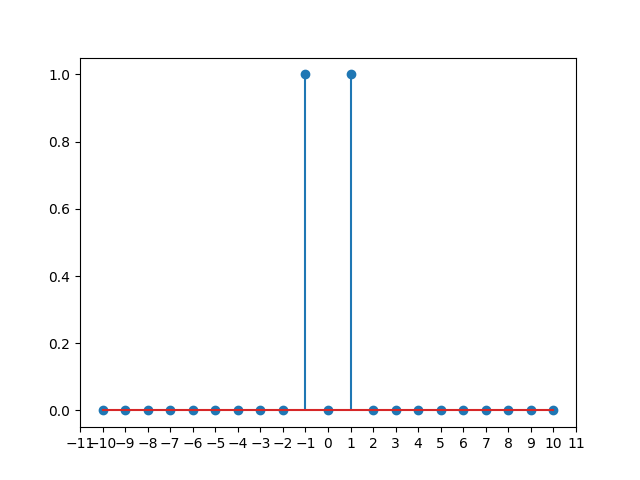
计算g=f(0)∗f(0):
g0=n=−∞∑∞fn(0)f−n(0)=2aag2=n=−∞∑∞fn(0)f2−n(0)=a2,g−2=a2
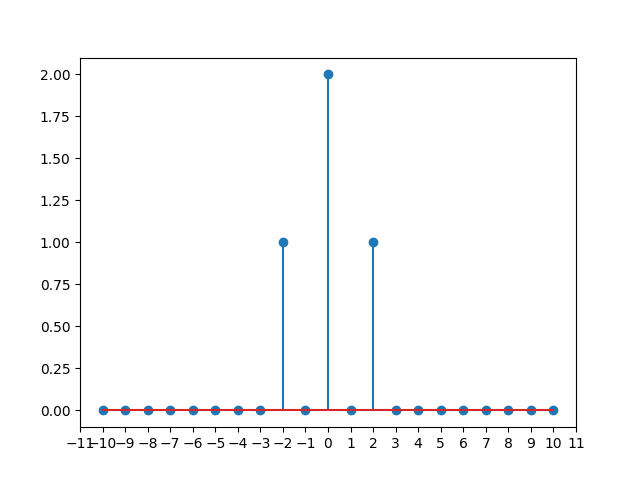
在此基础上计算h=f(0)∗f(0)∗f(0)=g∗f(0):
h3h−3h±1=n=−∞∑∞gn(0)f3−n(0)=a3,=n=−∞∑∞gn(0)f−3−n(0)=a3=3a2a,3aa2
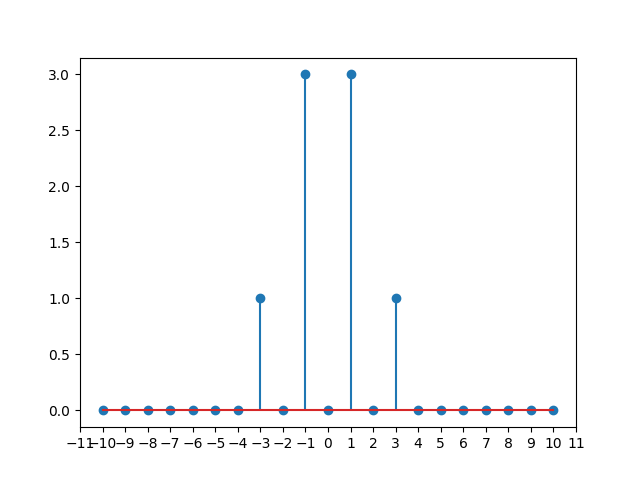
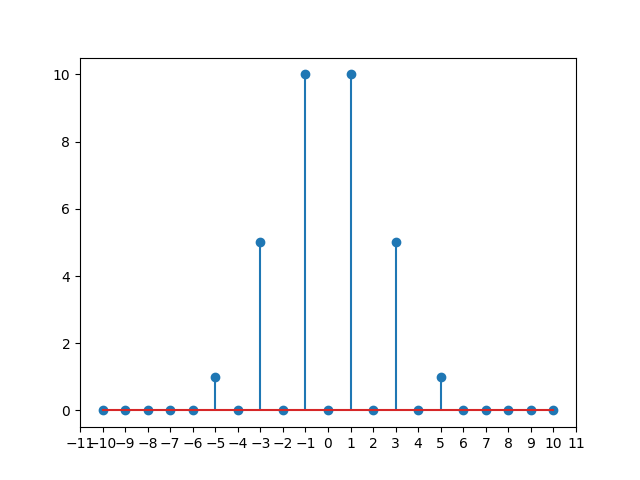
卷积计算可以不断地进行下去:
......
可以看出,对同一个函数地频谱进行多次卷积,会使得频谱由低频区向两侧的高频区扩展开来。这也是非线性谐振子频谱中高频项的来源。
计算
1.线性情形下的计算
当方程没有非线性项时:
x¨+ω02x=0
它的通解为:
x(t)=asin(ω0t)+bcos(ω0t)
或者写成复数形式:
x(t)=f1eiω0t+f−1e−iω0t
由于x是实数,所以f1=f−1∗
2.非线性情形的计算思路
当存在非线性项,且非线性项的能量远小于谐振子项时,我们假设它对fn和ω的影响也是很小的,所以可以写成:
fn=fn(0)+fn(1)+fn(2)+⋯ω=ω0+ω1+ω2+⋯
把它们和非线性项代入方程:
x¨+ω02x+Ax2+Bx3+⋯=0
0=dt2d2∑n=−∞∞(fn(0)+fn(1)+fn(2)+⋯)ein(ω0+ω1+ω2+⋯)t+ω02∑n=−∞∞(fn(0)+fn(1)+fn(2)+⋯)ein(ω0+ω1+ω2+⋯)t+A∑n=−∞∞(f(0)+f(1)+f(2)+⋯)∗(f(0)+f(1)+f(2)+⋯)nein(ω0+ω1+ω2+⋯)t+B∑n=−∞∞(f∗f∗f)nein(ω0+ω1+ω2+⋯)t
以上式子可以简写成:
n=−∞∑∞(−n2ω2fn+ω02fn+A(f∗f)n+B(f∗f∗f)n+⋯)einωt=0
左侧为傅里叶展开式,右边是零,由einωt的完备性知,左侧各项系数为0:
−n2ω2fn+ω02fn+A(f∗f)n+B(f∗f∗f)n+⋯=0∀n
−n2(ω0+ω1+ω2+⋯)2(fn(0)+fn(1)+fn(2)+⋯)+ω02(fn(0)+fn(1)+fn(2)+⋯)+A∑n=−∞∞(f(0)+f(1)+f(2)+⋯)∗(f(0)+f(1)+f(2)+⋯)n+⋯=0
将上式按大小阶数展开,相同阶数和为零,得到方程:
第零阶:(−n2+1)ω02fn(0)=0,∀n
第一阶:A(f(0)∗f(0))n+ω02fn(1)−2n2ω0ω1fn(0)−n2ω0fn(1)=0,∀n
第零阶
从第零阶中可以解出
{fn(0)=0,n=±1fn(0)=0,n=±1
由于x(t)为实数,fn=fn∗,不妨设f1(0)=a,f−1(0)=a
这对应线性项:
x(t)=2Re(a)cosω0t−2Im(a)sinω0t
第一阶
A(f(0)∗f(0))n+ω02fn(1)−2n2ω0ω1fn(0)−n2ω0fn(1)=0,∀n
第一阶中含有fn(1),ω1两个未知量。
当n±1时,方程中fn(1)前系数为零,方程中只剩下ω1,可以解出:
A(f(0)∗f(0))±1−2ω0ω1f±1(0)=0ω1=2ω0f±10A(f(0)∗f(0))±1
经过计算知道ω1=0
当n=±1时,代入ω1=0可以计算各个fn(1)的值:
fn(1)=(n2−1)ω02A(f(0)∗f(0))n(n=±1)
看起来我们无法计算f±1(1)的值,但因为第零阶中的a是人为规定的,故可以包含高阶下n=±1的微扰(相当于假设振动基频的振幅就是a,a)
因此我们不妨设f±1(1)=0
更高阶的一般性分析
第k阶的方程可以写作:
(−n2+1)ω02fn(k)−2fn(0)n2ω0ωk+λn(ω02,A1,⋯,Ak,ω1,⋯,ωk−1,fn(0),fn(1),⋯,fn(k−1))=0
在求第k阶之前,我们已经求得了ω1,⋯,ωk−1,fn(0),⋯,fn(k−1)的值,因此函数λn是已知项
计算自动化
可以看到,更高阶的计算十分繁琐,涉及的计算不仅项数极多,而且计算式中存在对无穷序列的多次离散卷积,很难处理。为了减少计算量,我们转向自动化符号计算工具(sympy),开发了一个计算各阶项参数的程序
一些重要的结果:
(下面设定f1(0)=a,f−1(0)=a)
ω1=0
f0(1)=−ω022A1aa
f2(1)=3ω02A1a2,f−2(1)=3ω02A1a2
ω2=6ω03a(−10A12+9A2ω02)a
f3(2)=12ω04A12a3+8ω02A2a3,f−3(2)=12ω04A12a3+8ω02A2a3
ω3=0
f0(3)=−9ω0638A13a2a2+ω0410A1A2a2a2−ω026A3a2a2
f2(3)=54ω0659A13a3a−12ω0431A1A2a3a+3ω024A3a3a,f−2(3)=54ω0659A13aa3−12ω0431A1A2aa3+3ω024A3aa3
f4(3)=54ω06A13a4+12ω04A1A2a4+15ω02A3a4,f−4(3)=54ω06A13a4+12ω04A1A2a4+15ω02A3a4
规律
(查看输出结果)
分别代入各Ai的情况
一些性质: