黎曼(内禀)曲率张量 #
把nabla算子推广到任意流形,其上可以没有度规,所以要分清矢量和对偶矢量。在推广 \(\vec\nabla\) 时它更像对偶矢量,故记作 \(\nabla_a\) 。
记 \(\mathscr F_M(k,l)\) 为流形M上全体 \(C^\infty\) 的 \((k,l)\) 型张量场集合(函数 \(f\) 视为标量场,因此 \(\mathscr F_M(0,0)=\mathscr F_M\) .)映射 \(\nabla:\mathscr F_M(k,l)\to\mathscr F_M(k,l+1)\) 称为M上的无挠导数算符,若它满足:
- 线性性: \(\nabla_a(\alpha T^{\bbb}{}_{\ccc}+\beta S^{\bbb}{}_{\ccc})=\alpha \nabla_a T^{\bbb}{}_{\ccc}+\beta\nabla_a S^{\bbb}{}_{\ccc}\)
- 满足Leibnitz律: \[\nabla_a(T^{\bbb}{}_{\ccc}S^{\ddd}{}_{\eee} )= T^{\bbb}_{\ccc}\nabla_a S^{\ddd}{}_{\eee} + S^{\ddd}{}_{\eee}\nabla_a T^{\bbb}{}_{\ccc}\]
- 与缩并可换序;
- \(v(f)=v^a\nabla_a f\) , \(\forall f\in\mathscr F_M,v\in \mathscr F_M(1,0)\) ;
- 无挠性(torsion-free): \(\nabla_a\nabla_b f=\nabla_b\nabla_a f,\forall f\in \mathscr F_M\)
条件3记作 \(\nabla\circ C=C\circ \nabla\) ,以后常写作
\[\nabla_a(v^b\omega_b)=v^b\nabla_a\omega_b+\omega_b\nabla_av^b\] 因为 \[\begin{aligned} \nabla_a(v^b\omega_b) &= \nabla_a[C(v^b\omega_c)]\\ &=C_2^1 [\nabla_a (v^b\omega_c)]\\&=C_2^1 (v^b\nabla_a\omega_c)+C_2^1[(\nabla_av^b)\omega_c] \\ &= v^b\nabla_a\omega_v+\omega_b\nabla_av^b \end{aligned}\]
条件4左侧不应写作 \(v^a(f)\) ,否则容易被误解为矢量场。条件4可在欧式空间 \(\mathbb{R}^3\) 下理解为: \[v^a=v^1\left({\partial \over\partial x}\right) ^a+v^2\left({\partial \over\partial y} \right)^a +v^3\left({\partial \over\partial z} \right)^a \\ v(f) = v^i\partial_i f = v^a\nabla_a f\] 可见条件4是这种性质对任意流形的推广
设 \(\nabla_a\) 是任意导数算符,则由条件4可得 \(\nabla_a f = (\mathrm{d} f)_a,\alpha f\in \mathscr F_M\) ( \((\mathrm{d} f)_av^a = \mathrm{d} f(v) =v(f)\overset{(4)}{=}v^a\nabla_a f\Rightarrow (\mathrm{d} f)_a = \nabla_a f\) )
任何流形必存在导数算符。事实上,导数算符存在且有多个。设 \(\nabla_a\) 和 \(\tilde\nabla_a\) 为两个导数算符,我们可推出它们作用于同一函数的结果相同: \(\nabla_a f=\tilde \nabla_a f=(\mathrm{d} f)_a, \forall f\in\mathscr F_M\) ,二者不同只能体现在非标量的标量场作用上。
设 \(p\in M\) , \(\omega_b,\omega_b' \in \mathscr F(0,1)\) 满足 \(\omega_b'|_p = \omega_b|_p\) ,则 \[[(\tilde{\nabla_a}-\nabla_a) \omega_b']_p = [(\tilde \nabla_a-\nabla_a) \omega_b]_p\] 证明略。
这说明,虽然导数 \([\nabla_a\omega_b]_p\) 依赖于 \(\omega_b\) 在p邻域内的取值,但导数的差 \([(\tilde\nabla_a -\nabla_a)\omega_b]_p\) 只依赖于 \(\omega_b\) 在p点的取值,说明 \(\tilde \nabla_a-\nabla_a\) 是把p点的 \((0,1)\) 对偶矢量 \(\omega_b|_p\) 变为p点的 \((0,2)\) 型张量的线性映射。给定p点的一个对偶矢量 \(\mu_a\) ,尽管把它延拓为矢量场 \(\omega_b\ \text{such that}\ \omega_b|_p=\mu_b\) 有很多种延拓方式,但再作用上 \(\tilde{\nabla}_a-\nabla_a\) 得到的 \((0,2)\) 型张量场就只有一种,因此这种延拓是自然的。 因而, \(\tilde{\nabla}_a-\nabla_a\) 作为一个映射,对应一个 \((1,2)\) 型张量 \(C^c{}_{ab}\) ,满足: \[[(\tilde\nabla_a-\nabla_a)\omega_b]_p =C^c{}_{ab} \omega_c|_p \\\] 即
对于 \((1,0)\) 型: \[\nabla_av^b = \tilde\nabla_av^b + C^b{}_{ac}v^c\] \((1,1)\) 型: \(\nabla_aT^b{}_c = \tilde\nabla_a T^b{}_{c}+C^b{}_{ad}T^d{}_{c}-C^e{}_{ac}T^b{}_{e}\)
给定O上的一个坐标 \(\{\xi^\mu\}\) ,在这组坐标下定义 \(\partial_a:\mathscr F_O(k,l)\to\mathscr F_O(k,l+1)\) ,以 \((1,1)\) 为例: \[\partial_a T^b{}_c := (\mathrm{d} x^\mu)_a \left({\partial \over\partial x^\nu } \right)^b \left(\mathrm{d} x^\sigma \right)_c\partial_\mu T^\nu{}_\sigma\] 其中坐标分量项的定义是 \(\partial_\nu T^\nu {}_\sigma={\partial T^\mu{}_{\sigma}\over\partial x^\mu }\) ,即“导数的坐标分量等于坐标分量的偏导数”
这种偏导算符只在这种坐标系下有定义,这叫做该坐标系的普通导数算符
与之对应的有协变导数算符(covariant derivative) \(\nabla_a\) ,它们与坐标系(或其他人为因素)无关。 普通导数算符作用与该系的任意坐标基矢和任一对偶坐标基矢结果为0: \(\partial_a(\partial/\partial x^\nu)^b = 0,\partial_a(\mathrm{d} x^\nu)_b=0\) 这时可以依据 \(\partial_a\) 表示 \(\nabla_a\) ,写出克氏符:
问题:“克氏符是不是张量?” 克氏符是否为张量和语境有关,称其为张量和非张量并不矛盾。 我们取定两个坐标系 \(\{x^\mu\}\) , \(\{x'^\mu\}\) ,可以分别诱导出两个克氏符 \(\Gamma^a{}_{bc},\bar\Gamma^a{}_{bc}\) 。二者关系如下:
| 诱导导数算符\表示坐标系 | \(\{x^\mu\}\) | \(\{x'^\nu\}\) | 符合坐标系变换? |
|---|---|---|---|
| \(\partial_a\mapsto \Gamma^a{}_{bc}\) | \(\Gamma^\sigma_{\mu\nu}(1)\) | \(\Gamma'^\sigma_{\mu\nu}(2)\) | 是 |
| \(\partial_a'\mapsto \bar\Gamma^a{}_{bc}\) | \(\bar\Gamma^\sigma_{\mu\nu}(3)\) | \(\bar\Gamma'^\sigma_{\mu\nu}(4)\) | 是 |
| 认为克氏符是张量可以作如下理解:在给定坐标系下的克氏符分别为(1)和(3),它们在基变换下满足张量变换律 \((1)\to(2),(4)\to(3)\) | |||
| 认为不是张量的人做了如下理解:在每个坐标系导数算符诱导出的克氏符必须在该坐标系下表示(只强调 \((1),(4)\) ),而 \((1)\lrArr(4)\) 不满足张量变换律。 |
克氏符是张量,但是依赖于坐标系的。与之类似地, \(\partial_a v^b\) 也是依赖于坐标系的张量: \(\partial_av^b\ne \partial_a' v^b\) 定义 \(v^\nu{}_{,\mu}\) 和 \(v^\nu{}_{;\mu}\) : \[\partial_av^b =(\mathrm{d} x^\mu)_a \left({\partial \over\partial x^\nu } \right)^b v^\nu{}_{,\mu} \\ \partial_a' v^b = (\mathrm{d} x'^\mu )_a \left({\partial \over\partial x'^\nu }\right)^b \partial'_\mu v'^\nu\] 用微分流形选定的 \(\nabla_a\) : \(\nabla_av^b =(\mathrm{d} x^\mu)_a\left({\partial \over\partial x^\nu } \right)^bv^\nu {}_{;\mu}\) 容易证明二者的关系为:
对易子与导数算符:对易子的定义 \([u,v]^a\) 不需要流形 \(M\) 有附加结构,但它的定义不能脱离被作用对象:标量场 \(f\) 。有了导数算符后就可以借助任意导数算符来写出它的显表达式:
\(\forall f\in \mathscr F\) ,借助 \(v(f)=v^a\nabla_a f\) ,有: \[\begin{aligned} [u,v] (f) &\equiv u(v(f))-v(u(f))\overset {(4)} = u^b\nabla_b (v^a\nabla_a f)-v^b\nabla_b (u^a\nabla_a f)\\ &\overset {(2),(3)}= u^b(\nabla_a v^a)\nabla_a f + v^au^b\nabla_b\nabla_a f-v^b(\nabla_b u^a)f - u^av^b\nabla_b\nabla_a f\\ &\overset{(5)}=(u^b\nabla_b v^a-v^b\nabla_b u^a)\nabla_a f\\ \end{aligned}\]
再由 \([u,v](f)=[u,v]^a\nabla_a f\) ,即可得证
3.2 矢量场沿曲线的导数和平移 #
3.2.1 矢量场沿曲线的平移 #
有了导数的微分流形中,我们可以讨论一个向量场是否是沿一条曲线平移的:
设 \(v^a\) 是沿曲线 \(C(t)\) 的矢量场, \(v^a\) 称为沿 \(C(t)\) 的平移[parallelly transported along C(t)],若 \(T^b\nabla_b v^a = 0,\) 其中 \(T^a\equiv(\partial/\partial t)^a\) 是曲线的切矢。
给定线上一点 \(C(t_0)\) 和这一点的 \(v^a|_{C(t_0)}\) ,能找到唯一一个沿线平移的向量场 \(v^a\)
\[\begin{aligned} T^b\nabla_b v^a &= T^b(\partial_b v^a+\Gamma^a{}_{bc}v^c)\\ &= T^b\left((\mathrm{d} x^\nu)_b \left({\partial \over\partial x^\mu } \right)^a \partial_\nu v^\mu +\Gamma^a{}_{bc}v^c\right)\\ &= T^\nu \left({\partial \over\partial x^\mu } \right)^a {\partial v^\mu \over\partial x^\nu } +\Gamma^a{}_{\nu\sigma}T^\nu v^\sigma(把重复抽象指标换成具体指标)\\ &= \left({\partial \over\partial x^\mu } \right)^a ({\partial v^\mu \over\partial x^\nu } T^\nu + \Gamma^\mu {}_{\nu\sigma}T^\nu v^\sigma)\\ 0&=\frac{\mathrm{d} v^\mu (t)}{\mathrm{d} t}+\Gamma^\mu{}_{\nu\sigma}T^\nu v^\sigma \end{aligned}\] 这是n个代求的一元函数 \(v^\mu(t)\) 满足的微分方程,可以用来求解这个矢量场。因此线上一点可以确定唯一的平移vector field
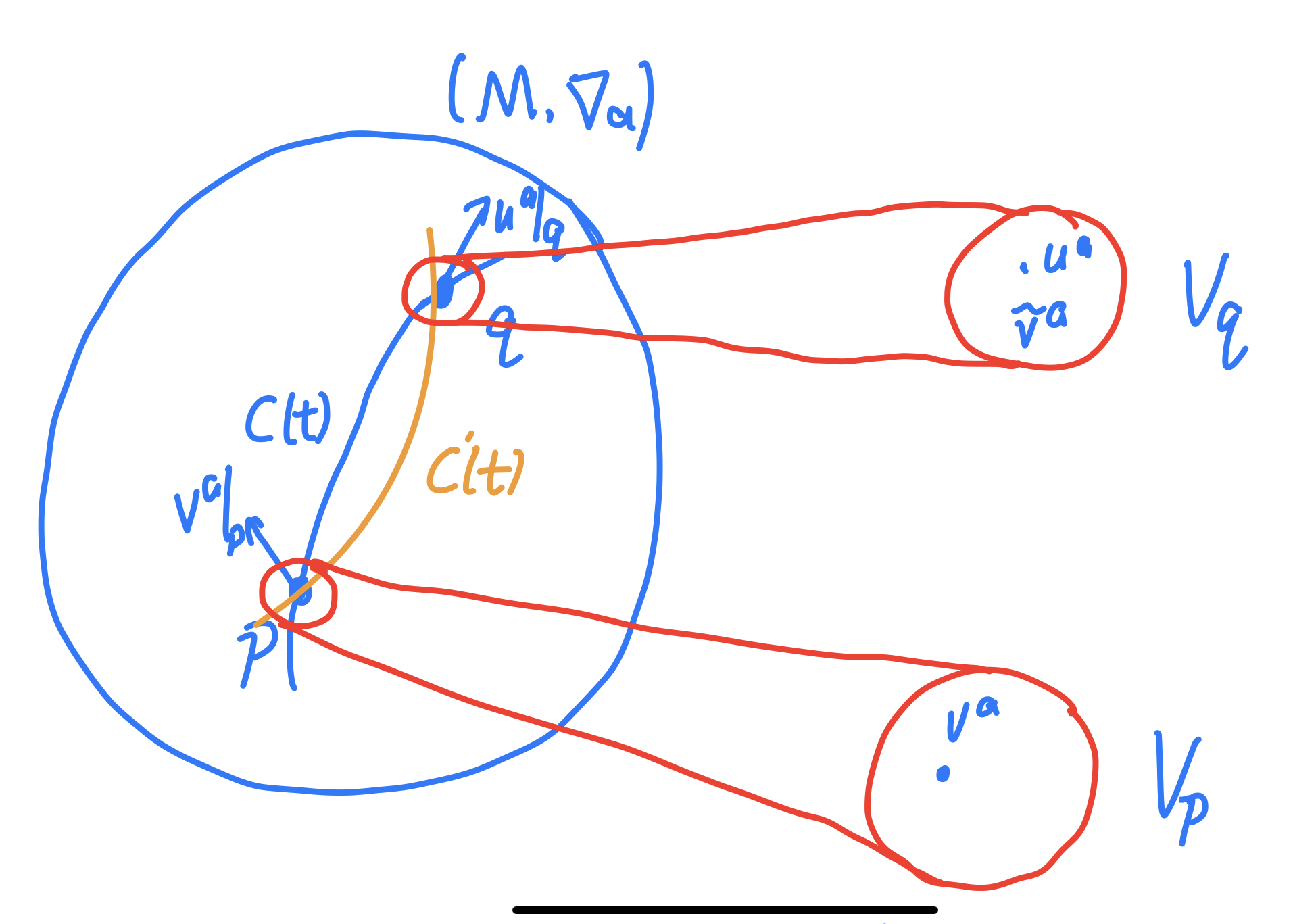 在一般流形中,我们不能谈及两个不同点的矢量
\(v^a|_{p},u^a|_{q}\)
是否相等,因为它们存在于两个不同的切空间
\(V_p,V_q\)
,如右图所示
在一般流形中,我们不能谈及两个不同点的矢量
\(v^a|_{p},u^a|_{q}\)
是否相等,因为它们存在于两个不同的切空间
\(V_p,V_q\)
,如右图所示
但当我们确定了导数
\(\nabla_a\)
后,我们可以从p到q画一条线
\(C\)
,把
\(v^a|_p\)
沿线平移到q点得到
\(\tilde v^a|_q\)
,然后比较
\(\tilde v^a|_q\)
是否等于
\(u^a|_{q}\)
。
但如果我们选一条不同的curve
\(C'\)
,得到的平移结果是否一样呢?并不总是如此。这叫做曲线相关的。一般只有欧氏、闵氏这样的简单空间中,平移才是曲线无关的。
这时我们发现,
\(\nabla_a\)
的存在为两个切空间建立了(哪怕是曲线相关的)联络(Connection)
3.2.2 与度规相适配的导数算符 #
如果我们再假设 \(M\) 上还选定了度规 \(g_{ab}\) ,矢量之间就可谈及内积。 为使得平移概念与欧式空间中熟知的平移一致,需要补充要求: \(u^a,v^a\) 是 \(C(t)\) 上矢量场, \(u^av_a\) 在 \(C(t)\) 上是常数(即两矢量平移时内积不变)。设 \(T^a\) 为 \(C(t)\) 的切矢,这一要求等价于 \[0=T^c\nabla_c(g_{ab}u^av^b)=g_{ab}u^aT^c\nabla_cv^b+g_{ab}v^bT^c\nabla_c u^a+u^av^bT^c\nabla_c g_{ab}=u^aT^bv^c \nabla_cg_{ab}\\\] 上式对任意的u和v成立,因此二者适配的充要条件为:
导数算符 \(\nabla_c\) 与度规 \(g_{ab}\) 适配,当且仅当 \(\nabla_c g_{ab} = 0\)
(注:由于平移性质 \(T^b\nabla_b u^a=0,T^b\nabla_b v^a=0\) ) 给定度规 \(g_{ab}\) ,一定存在唯一的 \(\nabla_c\) ,使得上式成立.
流形上选定度规场 \(g_{ab}\) 后,存在唯一的 \(\nabla_a\) 使得 \(\nabla_a g_{bc}=0\)
\[\begin{aligned} 0=\nabla_a g_{bc} &= \tilde\nabla_a g_{bc} -C^d{}_{ab}g_{dc} - C^d{}_{ac}g_{bd}\\ &= \tilde \nabla_a g_{bc}-C_{cab}-C_{bac} \end{aligned}\] 轮换指标,得到: \[\begin{aligned} C_{cab}+C_{bac}=\tilde\nabla_a g_{bc}\\ C_{cba}+C_{abc}=\tilde\nabla_b g_{ac}\\ C_{bac}+C_{acb} = \tilde\nabla_cg_{ab}\\ \end{aligned}\] 用 \((1)+(2)-(3)\) ,就得到适配的导数算符相对于 \(\tilde \nabla_a\) 的 \(C^a{}_{bc}\) 的表达式: \[C_{cab}=\frac 1 2 (\tilde\nabla_a g_{bc} +\tilde\nabla_b g_{ac} -\tilde\nabla_c g_{ab})\] 或: \[C^c{}_{ab} = \frac 1 2 g^{cd} (\tilde \nabla_a g_{bd}+\tilde \nabla_bg_{ad}-\tilde \nabla_dg_{ab})\] 这便是从非适配的导数算符得到适配导数算符的 \(C^c{}_{ab}\) 的方式,也是唯一解,因此只存在唯一与 \(g_{bc}\) 适配的导数算符。
给定 \(\nabla_a\) ,不存在唯一的度规 \(g_{ab}\) 与之适配
给定一组不适配的 \(\tilde \nabla_a\) 和 \(g_{bc}\) ,如何找到与度规适配的导数算符 \(\nabla_a\) ?上面的证明已经给出了答案。
继续证明的推导,用 \(\partial_a\) 充当 \(\tilde\nabla_a\) , \[\Gamma^c{}_{ab} = g^{cd}\Gamma_{dab} = \frac{1}{2}g^{cd} (\partial_ag_{bd}+\partial_bg_{ad}-\partial_dg_{ab})\] 用具体指标: \[\begin{aligned} \Gamma^\sigma{}_{\mu\nu} &= \Gamma^c{}_{ab} (\mathrm{d} x^\sigma)_c (\partial/\partial x^\mu)^a (\partial/\partial x^\nu)^b\\ &=\frac 1 2 g^{\sigma \rho}(g_{\nu\rho,\mu}+g_{\mu\rho,\nu}-g_{\mu\nu,\rho})\\ &=\frac 1 2 g^{\sigma\rho}(g_{\rho\mu,\nu}+g_{\nu\rho,\mu}-g_{\mu\nu,\rho})(指标不断轮换,好记) \end{aligned}\]
上式推导中用到:
- 重复抽象指标可直接化为具体指标: \(g^{cd} g_{bd}=g^{c\mu}g_{b\mu}\)
- 抽象指标的向实际指标的转换: \((\mathrm{d} x^\sigma)_c g^{cd}=(\mathrm{d} x^\sigma)_c (\partial/\partial x^\mu)^c g^{\mu d}=\delta^\sigma_\mu g^{\mu d}=g^{\sigma d}\)
3.2.3 矢量场沿曲线导数与沿曲线的平移之间的关系 #
考虑最简单的欧式空间。
\(p\) 点矢量 \(\vec {\tilde v}\) 称为 \(q\) 点的矢量 \(\vec v\) 平移至 \(p\) 点的结果,若二者在统一笛卡尔系的分量相等。
欧式空间中曲线 \(C(t)\) 上矢量场 \(\vec v\) 沿线导数 \(\mathrm{d} \vec v/\mathrm{d} t\) 定义为 \[\left.\frac{\mathrm{d} \vec v}{\mathrm{d} t}\right|_p:=\lim_{\Delta t\to 0} \frac{1}{\Delta t}(\vec {\tilde v}_p-\vec v|_p )\] 其中 \(\vec {\tilde v}|_p\) 是把 \(\vec v|_q\) 从线上邻点q平移到点p的结果, \(\Delta t\equiv t(q)-t(p),\forall p\in C(t)\)
可以证明, \(T^b\partial_bv^a\) 和 \(\mathrm{d} \vec v/\mathrm{d} t\) 相等。我们只需证明第 \(i\) 分量相等: \((\mathrm{d} x^i)_aT^b\partial_bv^a=T^b\partial_b(\mathrm{d} x^i)_a v^a=T^b\partial_b v^i=T(v^i)=\mathrm{d} v^i/\mathrm{d} t\) 将结论推广到任意 \(\nabla_a\) 的流形M的任意曲线,便将 \(T^b\nabla_b v^a\) 称为 \(v^a\) 沿 \(C(t)\) 的导数。有时也用 \(Dv^a/\mathrm{d} t\) 标记这一导数,即 \[D v^a/\mathrm{d} t \equiv T^b \nabla_b v^a\] . 这个定义没法推广到带有任意联络 \(\nabla_a\) 的流形,因为平移在一般的空间是曲线以来的。我们用导数 \(T^b\nabla_bv^a\) 定义了矢量 \(v^a\) 沿曲线的平移,但这么定义比较抽象。我们可以借助平移的概念反过来定义导数,即:
设 \(v^a\) 是沿 \((M,\nabla_a)\) 的曲线 \(C(t)\) 上的矢量场, \(T^b\) 是 \(C(t)\) 的切矢, \(p,q\) 是 \(C(t)\) 上邻点,则: \[T^b\nabla_b v^a|_p = \lim_{\Delta t\to 0}\frac 1 {\Delta t}(\tilde v^a|_p - v^a|_{p})\] 其中 \(\Delta t\equiv t(q)-t(p)\) , \(\tilde v^a|_p\) 是 \(v^a|_q\) 沿 \(C(t)\) 平移至 \(p\) 点的结果。
3.3 测地线 #
曲线 \(C(t)\) 的切矢 \(T^a\) 是 \(C(t)\) 上的矢量场。如果它本身是沿 \(C(t)\) 的平移,则这是一条测地线。
\((M,\nabla_a)\) 上的曲线 \(\gamma(t)\) 称为测地线(geodesic),若其切矢 \(T^a\) 满足 \(T^b\nabla_b T^a = 0\)
- 测地线的充要条件是其切矢沿线平移。
- \(T^b\nabla_b T^a = 0\) 称为测地线方程
- 若 \(M\) 上有度规场 \(g_{ab}\) ,则 \((M,g_{ab})\) 的测地线是指 \((M,\nabla_a)\) 的测地线,其中 \(\nabla_a\) 与 \(g_{ab}\) 适配
\(T^b\nabla_b v^a = T^b(\partial_b v^a+\Gamma^a{}_{bc}v^c)=0\) ,得到满足的微分方程: \(\mathrm{d} v^a/\mathrm{d} t+\Gamma^a{}_{bc}T^bv^c=0\) ,代入 \(v^a=T^a\) : \[\frac{\mathrm{d} T^\mu }{\mathrm{d} t}+\Gamma^\mu{}_{\nu\sigma} T^{\nu}T^{\sigma}=0\] 设测地线 \(\gamma(t)\) 的表达式为 \(x^\nu=x^\nu(t)\) ,则 \(T^\mu = \mathrm{d} x^\mu/\mathrm{d} t\) ,上式写为: \[\frac{\mathrm{d}^2 x^\mu }{\mathrm{d} t^2}+\Gamma^\mu {}_{\nu\sigma}\frac{\mathrm{d} x^\nu}{\mathrm{d} t}\frac{\mathrm{d} x^\sigma }{\mathrm{d} t}=0\] 下面举几个常用的例子:
- 欧式度规在笛卡尔系的克氏符为0,测地线方程通解为: \(x^\mu(t)=a^\mu t+b^\mu\) .因此测地线可以视作欧式空间中直线向广义黎曼空间的推广,在闵氏空间也有类似的结论。
- \(S^2\) 是三维欧式空间的二维球面,以球心为原点建系,三维欧式线元为 \(\mathrm{d} s^2=\mathrm{d} r^2+r^2(\mathrm{d} \theta^2+\sin^2\theta \mathrm{d} \phi^2)\) ,若线元在 \(S^2\) 上,则 \(r=R,\mathrm{d} r=0\) ,因此得到诱导线元 \(\mathrm{d} \hat s^2 = R^2(\mathrm{d} \theta^2+\sin^2\theta \mathrm{d} \phi^2)\) ,在坐标分量的度规 \(g_{\theta\theta}=R^2,g_{\phi\phi}=R^2\sin^2\theta,g_{\theta\phi}=g_{\phi\theta}=0\) ,测地线为大圆弧
设 \(\gamma(t)\) 为测地线,则其重参数化 \(\gamma'(t')=\gamma(t)\) 的切矢 \(T'^a\) 满足 \[T'^b\nabla_b T'^a = \alpha T'^a\]
\[T^a = \left({\partial \over\partial t} \right)^a = \frac{\mathrm{d} t'}{\mathrm{d} t}\left({\partial \over\partial t'} \right)^a\] 代入即得证
若曲线切矢 \(T^a\) 满足 \(T^b\nabla_b T^a = \alpha(t) T^a\) ,则存在 \(t'=t'(t)\) 使得 \(\gamma'(t')\) 为测地线。能将曲线变为测地线的参数叫该曲线的仿射参数(affine parameter)
\(t\) 为某测地线仿射参数,则该线任意参数 \(t'\) 是仿射参数的充要条件为 \(t'=at+b\)
给定流形上一点 \(p\) ,和这一点的一个切矢 \(v^a\) ,则存在唯一的测地线过该点且切矢等于 \(v^a\) ,简称“一点一矢定一测”
之前已经给出测地线满足的常微分方程组 \[\frac{\mathrm{d} ^2x^\mu }{\mathrm{d} t^2}+\Gamma^\mu{}_{\nu\sigma} \frac{\mathrm{d} x^\nu}{\mathrm{d} t}\frac{\mathrm{d} x^\sigma }{\mathrm{d} t}=0\] 给出的点p和切矢,可以看成给出了二阶常微分方程的一点值和一阶导数(即初始条件),根据常微分方程理论,我们可以确定唯一一个解。
因为切矢 \(T^a\) 沿测地线平移,故内积 \(g_{ab}T^aT^b\) 为常数。证明可考虑 \(T^c\nabla_c(g_{ab}T^aT^b)\) 是否为零: \[\begin{aligned} &T^c\nabla_c(g_{ab}T^aT^b)\\ =&\nabla_c(g_{ab})T^cT^aT^b+T^ag_{ab}T^c\nabla_cT^b+T^bg_{ab}T^c\nabla_cT^a \\ =&0 \end{aligned}\] (5)中第一项导数算符与度规适配,因此为 \(0\) ;后两项为测地线切矢沿自身平移的性质 因此, \(g_{ab}T^aT^b\) 只会恒正、恒负或恒为0,不存在分段类时/类空的测地线
在欧式空间中,两点之间线段最短;但在黎曼空间中,是否有类似的结论?
设 \(g_{ab}\) 是流形M上的洛伦兹度规场, \(p,q\in M\) ,则 \(p,q\) 之间的光滑类空(类时)曲线为测地线当且仅当其线长取极值。
一元函数取极值可以是极小值 \(f''(x)>0\) ,极大值 \(f''(x)<0\) ,或既非极小值又非极大值 \(f''(x)=0\) ,线长也有三种可能: 对 \(g_{ab}\) 正定的情况, \(p,q\) 之间曲线长度一定不会是极大值,取了最小值的一定是测地线,但测地线不一定是取最小值的曲线。
对洛伦兹度规的情况,考虑二维闵氏空间
\((\mathbb{R}^2,\eta_{ab})\)
,
\(\eta_{ab} = \eta_{\mu\nu}(\mathrm{d} x^\mu)_a(\mathrm{d} x^\nu)_b\)
,线元为
\(\mathrm{d} s^2 = \eta_{\mu\nu}\mathrm{d} x^\mu\mathrm{d} x^\nu=-(\mathrm{d} x^0)^2+(\mathrm{d} x^1)^2\)
,对于类时联系的两点,有线长
\(l=\int_p^q \sqrt{-\mathrm{d} s^2}\)
。我们总可以把两点通过洛伦兹变换将其均落在时间轴上。
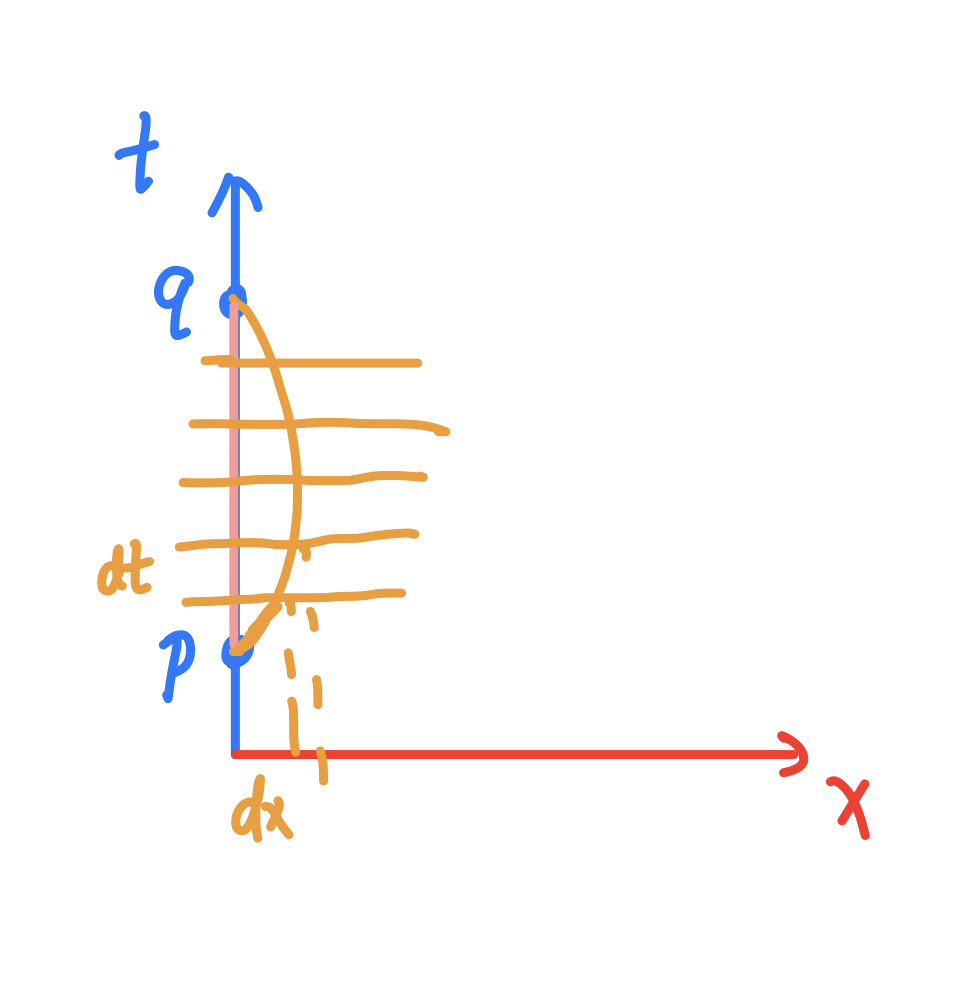 如上图所示,粉色的测地线
\(C_1\)
与近邻的橙色曲线
\(C_2\)
比较,有:
\[\int_{C_2}\sqrt{-\mathrm{d} s^2}=\int_{C_2}\sqrt{-(-\mathrm{d} t^2+\mathrm{d} x^2)}<\int_{C_1}\sqrt{\mathrm{d} t^2}=t_q-t_p\]
即,此时测地线取极大值
如上图所示,粉色的测地线
\(C_1\)
与近邻的橙色曲线
\(C_2\)
比较,有:
\[\int_{C_2}\sqrt{-\mathrm{d} s^2}=\int_{C_2}\sqrt{-(-\mathrm{d} t^2+\mathrm{d} x^2)}<\int_{C_1}\sqrt{\mathrm{d} t^2}=t_q-t_p\]
即,此时测地线取极大值
3.4 黎曼曲率张量 #
导数算符无挠性保证 \([\nabla_a,\nabla_b]f=0\) ,但对矢量场和更高阶的张量场未必为0.黎曼曲率张量是用来衡量这种非对易性的量。
容易证明, \[[\nabla_a,\nabla_b](f\omega_c)=f[\nabla_a,\nabla_b]\omega_c\]
下面的定理说明,导数算符的对易子作用于矢量场上,值只与矢量场的这一点有关,因此可以像克氏符一样做线性展开:
设 \(\omega_c,\omega_c'\in\mathscr F(0,1)\) ,且 \(\omega'_c|_p=\omega_c|_p\) ,则 \[[[\nabla_a,\nabla_b]\omega_c']|_{p} = [[\nabla_a,\nabla_b]\omega_c]|_p\]
定义黎曼曲率 \(R_{abc}{}^d\) 为 \[(\nabla_a\nabla_b-\nabla_b\nabla_a)\omega_c = R_{abc}{}^d\omega_d, \quad \forall\omega_c\in\mathscr F(0,1)\]
欧式空间和闵氏空间的黎曼曲率张量场为0.
欧/闵式空间任意笛卡尔/洛伦兹系的普通导数算符 \(\partial_a\) 是与 \(\delta_{bc}\) 适配的导数算符,而 \[(\partial_a\partial_b-\partial_b\partial_a)\omega_c = (\mathrm{d} x^\mu)_a(\mathrm{d} x^\nu)_b(\mathrm{d} x^\sigma)_c (\partial_\mu\partial_\mu\omega_\sigma-\partial_\nu\partial_\mu\omega_\sigma)=0\]
因此称欧式空间和闵氏空间都是平直空间。闵氏空间类似于欧式空间,因此称为伪欧空间。
随意取 \(\omega_c\in\mathscr F(0,1)\) 与 \(v^c\) 缩并形成标量,作用导数对易子应为0: \[\begin{aligned} 0&=(\nabla_a\nabla_b-\nabla_b\nabla_a)(v^c\omega_c) \\&= v^c[\nabla_a,\nabla_b]\omega_c+\omega_c[\nabla_a,\nabla_b]v^c\\ \omega_c[\nabla_a,\nabla_b]v^c &= -v^cR_{abc}{}^d\omega_d\\ [\nabla_a,\nabla_b]v^c &= -R_{abd}{}^cv^d\\ \end{aligned}\]
黎曼曲率的性质
- \(R_{abc}{}^d = -R_{bac}{}^d\)
易证。
- 循环恒等式: \(R_{[abc]}{}^d=0\)
对任意 \(\omega_d\) ,有: \[R_{[abc]}{}^d\omega_d = \nabla_{[a}\nabla_b\omega_{c]}-\nabla_{[b}\nabla_a\omega_{c]} = 2\nabla_{[a}\nabla_b\omega_{c]}\] 即证 \[\nabla_{[a}\nabla_b\omega_{c]}=0\] 令 \(\tilde \nabla_a = \partial_a\) ,得到: \[\begin{aligned} \nabla_a(\nabla_b\omega_c)&=\partial_a(\nabla_b\omega_c)-\Gamma^d{}_{ab}\nabla_d\omega_c-\Gamma^d{}_{ac}\nabla_b\omega_d \\ &= \partial_a(\partial_b-\Gamma^e{}_{bc}\omega_e)-\Gamma^d{}_{ab}\nabla_d\omega_c-\Gamma^d{}_{ac}\nabla_b\omega_d \\ \nabla_{[a}\nabla_b\omega_{c]} &= \partial_{[a}\partial_b\omega_{c]}-\partial_{[a}\omega_{|e|}\Gamma^e{}_{bc]}-\omega_e\partial_{[a}\Gamma^{e}{}_{bc]}-\Gamma^d{}_{[ab}\nabla_{|d|}\omega_{c]}-\Gamma^{d}{}_{[ac}\nabla_{b]}\omega_d\\ &=0 \end{aligned}\] 最后一步用到 \(\Gamma^e_{bc}=\Gamma^e{}_{cb},\partial_a\partial_b=\partial_b\partial_a\)
- Bianchi恒等式: \(\nabla_{[a}R_{bc]d}{}^e=0\)
若存在度规场 \(g_{ab}\) ,且与导数适配: \(\nabla_ag_{bc}=0\) ,定义 \(R_{abcd}\equiv g_{de}R_{abc}{}^e\) 则曲率张量还有性质:
- \(R_{abcd}=-R_{abdc}\)
- \(R_{abcd} = R_{cdab}\)
定义 \((0,2)\) 型张量的trace为经过度规升降后的(1,1)型张量的trace: \[T_{ab}\to T^a{}_b = g^{ac}T_{cb}\\ T^a{}_a = g^{ac}T_{ca}\] 对于四阶曲率张量,可以定义 \(C^2_4=6\) 种trace: \[g^{ab}R_{abcd},\\ g^{ac}R_{abcd},\\ g^{ad}R_{abcd},\\ g^{bc}R_{abcd},\\ g^{bd}R_{abcd},\\ g^{cd}R_{abcd}\] 但由于前两指标和后两指标分别反对称,第一个和第六个一定=0;同时有第2个=第5个,第3个=第4个。同时第3、4个+第2、5个=0,因此曲率张量只有一种独立的缩并。记 \[g^{ac}R_{abcd}\equiv R_{bd}\\ g^{bd}R_{abcd}\equiv R_{ac}\] \(R_{ac}\) 称为里奇(Ricci)张量。如果在流形上没有定义度规 \(g_{ab}\) ,我们能否定义里奇张量?答案是肯定的。因为曲率张量 \(R_{abc}{}^d\) 天生为(1,3)型张量,可以直接定义缩并 \(R_{ac}\equiv R_{abc}{}^b\) 记 \(R \equiv g^{ac}R_{ac}\) 为标量曲率(Scalar Curvature),它的定义依赖于度规。 此外,还应掌握 \(R_{abc}{}^d\) 的无迹部分,叫做Weyl张量: \[C_{abcd} \equiv R_{abcd}-\frac{2}{n-2}(g_{a[c}R_{d]b}-g_{b[c}R_{d]a}) + \frac{2}{(n-1)(n-2)}Rg_{a[c}g_{d]b}\]
广义黎曼空间的爱因斯坦张量 \(G_{ab}\) 定义为: \[G_{ab}\equiv R_{ab} -\frac 1 2 Rg_{ab}\]
3.4.2 由度规计算黎曼曲率 #
在 \((M,g_{ab})\) 上选定一个基底场,由度规可以决定唯一的联络 \(\nabla_a\) ,因而有确定的黎曼张量 \(R_{abc}{}^d\) .下面计算它的分量。
坐标: \(\{x^\mu\}\) 坐标基底场: \(\{({\partial \over\partial x^\mu } )^a\}\) ,坐标基底场之间的分量一定对易。 对偶坐标基底场: \(\{(\mathrm{d} x^\mu)_a\}\) 某个非坐标基底场: \(\{(e_\mu)^a\},\{(e^\mu)_a\}\)
对于平面极坐标系,坐标 \(r,\theta\) ,基底场 \({\partial \over\partial r} ,{\partial \over\partial \theta}\) ,这时它不是正交归一的( \(\frac{1}{r}{\partial \over\partial \theta }\) 是归一矢),但归一化后的矢量不是对易的。
\[\begin{aligned} \nabla_a\nabla_b\omega_c &= \partial_a\nabla_b\omega_c-\Gamma^d{}_{ab}\nabla_d\omega_c-\Gamma^d{}_{ac}\nabla_b\omega_d\\ &=(\partial_a(\partial_b\omega_c-\Gamma^e{}_{bc}\omega_e))-\cdots\\ &=\partial_a\partial_b\omega_c-\Gamma^e{}_{bc}\partial_a\omega_e-\omega_e\partial_a\Gamma^e{}_{bc}-\Gamma^d{}_{ab}\nabla_d\omega_c-\Gamma^d{}_{ac}(\partial_b\omega_d-\Gamma^e{}_{bd}\omega_e) \end{aligned}\] 对a,b做反对称: \[\begin{aligned} \nabla_{[a}\nabla_{b]}\omega_c &=\partial_{[a}\partial_{b]}\omega_c-\Gamma^e{}_{c[b}\partial_{a]}\omega_e-\omega_e\partial_{[a}\Gamma^e{}_{b]c}-\Gamma^d{}_{[ab]}\nabla_d\omega_c-\Gamma^d{}_{c[a}(\partial_{b]}\omega_d-\Gamma^e{}_{b]d}\omega_e)\\ &= -\partial_{[a}\Gamma^e{}_{b]c}\omega_e+\Gamma^d{}_{c[a}\Gamma^e{}_{b]d}\omega_e\\ &= -\partial_{[a}\Gamma^d{}_{b]c}\omega_d+\Gamma^e{}_{c[a}\Gamma^d{}_{b]e}\omega_d \end{aligned}\] 第1、4项为0,第二项和第五项相消,原式为: \[\begin{aligned} R_{abc}{}^d\omega_d&=2\nabla_{[a}\nabla_{b]}\omega_c\\ &=-2(\partial_{[a}\Gamma^d{}_{b]c}\omega_d-\Gamma^e{}_{c[a}\Gamma^d{}_{b]e}\omega_d),\forall \omega_d\\ R_{abc}{}^d&=-(\partial_a\Gamma^d{}_{bc}-\partial_b\Gamma^d{}_{ac})+\Gamma^e{}_{ca}\Gamma^d{}_{be}-\Gamma^e{}_{cb}\Gamma^d{}_{ae}\\ R_{\mu\nu\sigma}{}^\rho &= \partial_{\nu}\Gamma^\rho{}_{\mu\sigma}-\partial_\mu\Gamma^\rho{}_{\nu\sigma}+\Gamma^{\lambda}{}_{\sigma\mu}\Gamma^\rho{}_{\nu\lambda}-\Gamma^\lambda{}_{\sigma\nu}\Gamma^{\rho}{}_{\mu\lambda} \end{aligned}\] 由 \(g_{\mu\nu}\) 计算 \(\Gamma^\rho{}_{\mu\sigma}=\frac 1 2 g^{\rho\nu}(g_{\nu\mu,\sigma}+g_{\sigma\nu,\mu}-g_{\mu\sigma,\nu})\) ,然后就能得到 \(R_{\mu\nu\sigma}{}^\rho\) 的值
- 若度规 \(g_{ab}\) 在某坐标系分量全为常数,则其克氏符全为0: \(\Gamma^\sigma{}_{\mu\nu} = 0\) ,从而黎曼张量 \(R_{abc}{}^d=0\) ,因而在坐标域内是平直度规。反之,若已知 \(R_{abc}{}^d=0\) ,也一定存在坐标系使 \(g_{ab}\) 坐标分量为常数,证明略。
- 可以由克氏符的缩并 \(\Gamma^\mu{}_{\mu\sigma}\) 计算任意坐标系下的散度公式 \(\vec \nabla \cdot \vec v=\nabla_av^a\) 。