5.1 微分形式 #

先介绍 \(n\) 维空间 \(V\) 上的形式，再讨论 \(n\) 维流形 \(M\) 上的微分形式场。

由定义知，1形式就是 \(V\) 上对偶矢量, \(\Lambda(1)=V^*\) .约定把任意实数称为 \(V\) 上0形式，则 \(\lambda(0)=\mathbb{R}\) 若微分形式某分量有两个指标重复，则整个分量为0. 记 \(\mathscr{T}_{V}(0,l)\) 是全体(0,l)型矢量空间的集合，全体l-form的集合记为 \(\Lambda(l)\) ，则 \(\Lambda(l)\subset \mathscr{T}_{V}(0,l)\)

\[\dim \Lambda(l) = \begin{cases} \frac{n!}{l!(n-l)!},& l\ge n\\ \\ 0, & l<n \end{cases}\] proof:对 \(n=3,l=2\) 情形， \[\begin{aligned} \omega_{ab}&=\omega_{11}(e^1)_{a}(e^1)_{b} + \omega_{12}(e^1)_{a}(e^2)_{b}+\omega_{13}(e^1)_{a}(e^3)_{b}+\dots \\ \\ &= \omega_{12}(e^1)_{a}\wedge(e^2)_{b}+\omega_{13}(e^1)_{a}\wedge (e^3)_{b}+\omega_{23}(e^2)_{a}\wedge(e^3)_{b} \\ \end{aligned}\] 推广到一般情形，就有： \[\omega_{ab}=\sum_{C}\omega_{\mu\nu}(e^\mu)_{a}\wedge (e^\nu)_{b}\\ \omega_{a_{1}\dots a_{l}}=\sum_{C}\omega_{\mu_{1}\dots\mu_{l}}(e^{\mu_{1}})_{a_{1}}\wedge \dots\wedge (e^{\mu_{l}})_{a_{l}}\] 其中 \(\sum_{c}\) 表示对 \(n\) 个数中取 \(l\) 个数的各种组合求和，即， \(\Lambda(l)\) 的基底矢量共 \(C_n^l\) 个 当 \(l<n\) 时， \(\Lambda(l)\) 一定有重复指标，因而只有零元一个元素。

\(\omega_{a_{1}\dots a_{l}}=\sum_{C}\omega_{\mu_{1}\mu_{2}\dots \mu_{l}}(\mathrm{d}x^{\mu_{1}})_{a_{1}}\wedge \dots\wedge(\mathrm{d}x^{\mu_{l}})_{a_{l}}\) 其中的每个分量可以写成： \(\omega_{\mu_{1}\dots \mu_{l}}=\omega_{a_{1}\dots a_{l}}\left( \frac{ \partial }{ \partial x^{\mu_{1}} } \right)^{a_{1}}\dots(\frac{ \partial }{ \partial x^{\mu_{l}}})^{a_{l}}\) 注意里面逆变坐标基矢之间是张量积而不是楔积。

或者说，楔积是满足上式的映射 \(\wedge:\Lambda(l)\times \Lambda(m)\to \Lambda(l+m)\) ,楔积 \((\omega\wedge \mu)_{a_{1}\dots a_{l}b_{1}\dots b_{m}}\) 可记作 \(\omega_{a_{1}\dots a_{l}}\wedge \mu_{b_{1}\dots b_{m}}\) ，常简记为 \(\mathbf{ \omega}\wedge \mathbf{ \mu}\) 楔积满足结合律和分配律： \(( \omega\wedge \mu )\wedge \nu=\omega \wedge(\mu\wedge \nu),\omega \wedge (\mu+\nu)=\omega \wedge \mu+\omega\wedge \nu\) 但楔积不服从分配律。例如，对两个1-form有： \[\omega\wedge \mu=(\omega\wedge\mu)_{ab}=\omega_{a}\mu_{b}-\omega_{b}\mu_{a}\] \[\mu\wedge \omega=\mu_{a}\omega_{b}-\mu_{b}\omega_{a}\] 即两个1-form满足反交换律。对一般情况， \(\omega,\mu\) 分别为 \(l,m\) 形式，则 \[\omega\wedge \mu=(-1)^{lm}\mu\wedge\omega\] 回到流形上讨论。若 \(M\) 上任一点 \(p\) 指定一个 \(V_p\) 上的l-form, 就得到 \(M\) 上的 \(l\) 形式场。 \(M\) 上光滑的 \(l\) 形式场称为l次微分形式场，也称作 \(l\) 形式场或 \(l\) 形式 取定坐标系 \((O,\psi)\) ,则 \(O\) 上 \(l\) 形式场可方便的用对偶坐标基底场逐点线性表出。

定义外微分算符 \(d:\Lambda_M(l)\to\Lambda_M(l+1)\) ： \[(\mathrm{d} \omega)_{ba_1\cdots a_l}:=(l+1)\nabla_{[b}\omega_{a_1\cdots a_l]}\] 注意，这时导数算符的任意性不影响结果： \[\nabla_b\omega_a = 2\nabla_{[b}\omega_{a]}=2\tilde\nabla_{[b}\omega_{a]}+\Gamma^{c}{}_{[ba]}\omega_c=2\tilde\nabla_{[b}\omega_{a]}\] 此时，我们就可以将 \((\mathrm{d} f)_b=\nabla_b f\) 看成0-form的外微分。 对l-form \(\omega_{ba_1\cdots a_l}\) 做外微分，把系数看成张量场，得到： \[(\mathrm{d}\omega)_{ba_1\cdots a_l} = \sum_C(\mathrm{d} \omega_{\mu_1\cdots a_l})_b\wedge (\mathrm{d} x^{\mu_1})_{a_1}\wedge\cdots \wedge (\mathrm{d} x^{\mu_l})_{a_l}\]

容易知道，恰当形式一定是闭形式。那么闭形式是否为恰当形式呢？答案是否。这个命题正确与否与具体的流形有关：比如，对 \(\mathbb{R}^n\) 流形，该命题正确。对任意流形，这个命题为是局域恰当的：即对任一点p，存在邻域U，在U上可找到场 \(\mu\) 使得 \(\mathrm{d} \mu=\omega\)

推论： \(M=\mathbb{R}^2\) 时，定理5-1-5给出命题：给定函数 \(X(x,y),Y(x,y)\) , \(\exists f(x,y)\) 使得 \(\mathrm{d} f=X\mathrm{d} x+Y\mathrm{d} y\) 当且仅当 \({\partial X\over\partial y} ={\partial Y\over\partial x}\)

5.2 流形上的积分 #

三维空间中，要计算线积分和面积分都要指定一个方向。未确定方向的积分会有正负号的差异。推而广之，计算任意流形上的积分都应指定该流形的定向。

为说明定义的合理性，应证明 \(\omega\) 在G上的积分与所选右手坐标系无关。取二维流形中的两个坐标系 \(x^\mu,x^\mu{}'(\mu = 1,2)\) ，则 \[\omega = \omega_{12}\mathrm{d} x^1\wedge \mathrm{d} x^2 = \omega_{12}'\mathrm{d} x'^1\wedge \mathrm{d} x'^2\] 令 \(\int_G\omega \equiv \int_{\psi [G]}\omega_{12}\mathrm{d} x^1\mathrm{d} x^2,(\int_G\omega)' \equiv \int_{\psi [G]} \omega_{12}'\mathrm{d} x'^1\mathrm{d} x'^2\) ，欲证 \[(\int_G\omega)' = \int_G\omega\] 由张量变换律， \[\begin{aligned} \omega_{12}' & =\omega_{ab}\left( \frac{ \partial }{ \partial x'^1 } \right)^a \left( \frac{ \partial }{ \partial x'^2 } \right)^b \\ &=\omega_{ab}\left[ \left( \frac{ \partial x^1 }{ \partial x'^1 } \right)^a \left( \frac{ \partial }{ \partial x^1 } \right)^a +\left( \frac{ \partial x^1 }{ \partial x'^2 } \right)\left( \frac{ \partial }{ \partial x^2 } \right)^a \right]\left[ \left( \frac{ \partial x^1 }{ \partial x'^2 } \right)\left( \frac{ \partial }{ \partial x^1 } \right)^b+\left( \frac{ \partial x^2 }{ \partial x'^2 } \right)\left( \frac{ \partial }{ \partial x^2 } \right)^b \right] \\ &= \omega_{\mu\nu} \frac{ \partial x^\mu }{ \partial x'^1 } \frac{ \partial x^\nu }{ \partial x'^2 } \\ &= \omega_{12} \frac{ \partial x^1 }{ \partial x'^1}\frac{ \partial x^2 }{ \partial x'^2 } +\omega_{21}\frac{ \partial x^2 }{ \partial x'^1 } \frac{ \partial x^1 }{ \partial x'^2 } \\ &= \omega_{12}\det\left( \frac{ \partial (x^1,x^2) }{ \partial (x'^1,x'^2) } \right) \end{aligned}\] 再由坐标变换的Jacob公式，得到的行列式相消即可得证。

今后谈及 \(l\) 形式场 \(\mu\) 在l维子流形 \(\phi [S]\) 上的积分时，一律理解为 \(\mu\) 的限制 \(\tilde \mu\) 的积分: \(\int_{\phi [S]}\mu \equiv \int_{\phi [S]}\tilde \mu\)

5.3 Stokes定理 #

先引入带边流形的概念：带边流形最简单的例子是

\(\mathbb{R}^{n-}=\{(x^1\cdots x^n)\in \mathbb{R}^n|x^1\le 0\}\) \(x^1=0\) 为其边界，是 \(n-1\) 维流形。推广至一般情况， \(n\) 维带边流形 \(N\) 与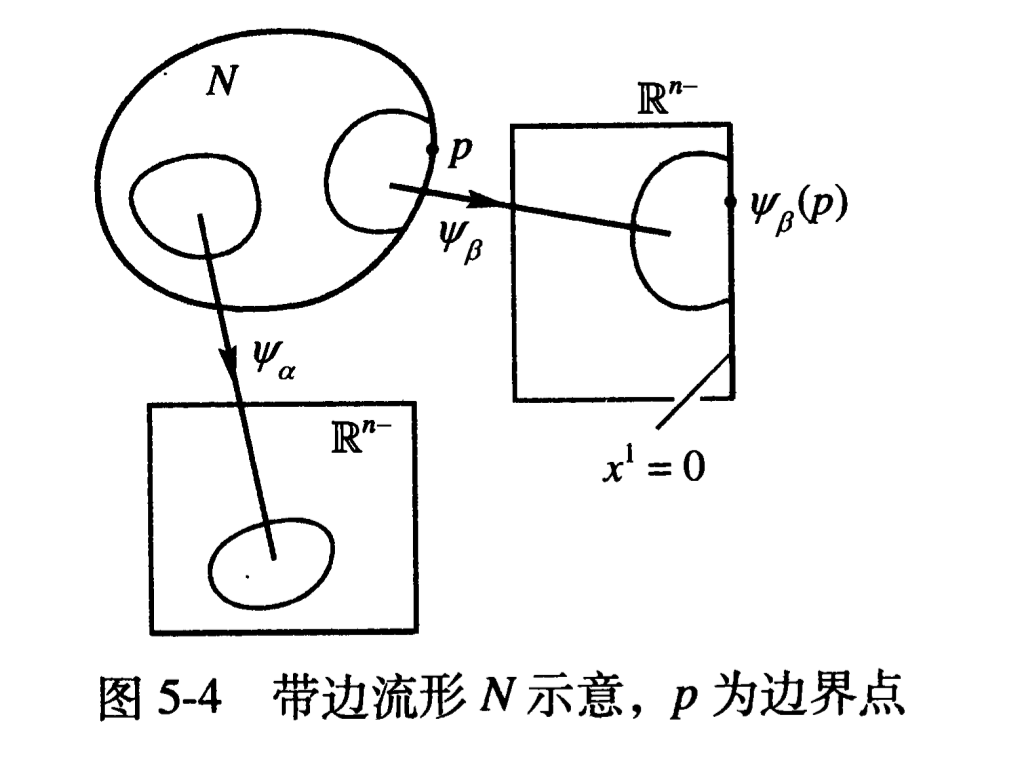普通流行的定义相仿，只是将定义中的 \(\mathbb{R}^n\) 改为了 \(\mathbb{R} ^{n-}\) :带边流形 \(N\) 的开覆盖 \(\{O_\alpha\}\) 中每一元素 \(O_\alpha\) 都同胚于 \(\mathbb{R}^{n-}\) 的一个开子集， \(N\) 中全体被映射到 \(x^1=0\) 处的点集组成 \(N\) 的边界 \(\partial N\) ,这是一个 \(n-1\) 维流形；N的内部 \(i(N)=N-\partial N\) 是 \(n\) 维流形. 例如， \(B\) 是三维带边流形，内部 \(i(B)\) 是三维流形，边界 \(S^2\) 是二维流形

例：考虑 \(\mathbb{R}^2\) 上的Stokes定理， \[\iint_S\left(\partial A_2 / \partial x^1-\partial A_1 / \partial x^2\right) \mathrm{d} x^1 \mathrm{~d} x^2=\oint_L A_l \mathrm{~d} l\] 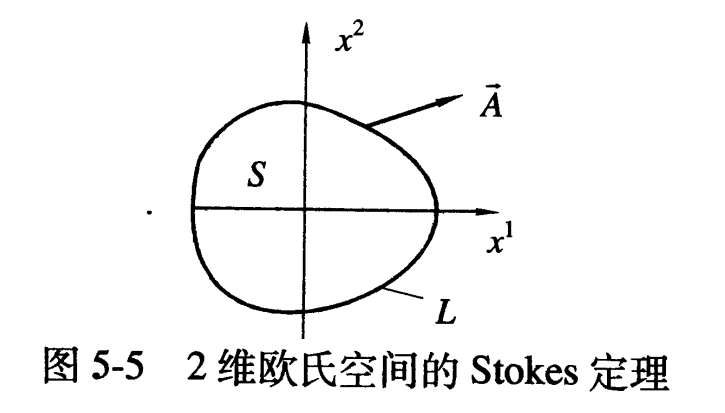用欧式度规把 \(A^a\) 变为1-form \(A_a = \delta_{ab}A^b,\) 则 \(A_a\) 可充当Stokes定理中的 \(\omega\) 。把 \(A_a\) 用笛卡尔系对偶坐标基矢展开： \(\omega = A_a = A_\mu (\mathrm{d} x^\mu)_a\) , \[\begin{aligned} \mathrm{d} \omega &= \mathrm{d} A_\mu \wedge \mathrm{d} x^\mu = {\partial A_\mu \over\partial x^\nu}\mathrm{d} x^\nu \wedge \mathrm{d} x^\mu = {\partial A_1\over\partial x^2} \mathrm{d} x^2\wedge \mathrm{d} x^1+{\partial A_2\over\partial x^1} \mathrm{d} x^1\wedge \mathrm{d} x^2\\ &= \left({\partial A_2\over\partial x^1} -{\partial A_1\over\partial x^2} \right)\mathrm{d} x^1\wedge \mathrm{d} x^2 \end{aligned}\] 所以左侧可表为 \(\int_{i(N)}\mathrm{d} \omega=\iint (\partial A_2/\partial x^1-\partial A_1/\partial x^2)\mathrm{d} x^1\mathrm{d} x^2\) ,即Stokes公式左侧特例。另一方面，Stokes公式右面为 \(\int_{\partial N}\omega=\int_{\partial N}\tilde \omega\) ,选线长 \(l\) 为 \(L\) 局部坐标，按Stokes公式把 \(\tilde \omega\) 用坐标基矢展开为 \(\tilde \omega_a = \tilde \omega_1(l)(\mathrm{d} l)_a\) ，两边和 \((\partial/\partial l)^a\) 缩并： \[\tilde \omega_1(l) = \tilde \omega_a (\partial/\partial l)^a = \omega_a(\partial/\partial l)^a = A_a (\partial/\partial l)^a = A_l\] 于是 \(\tilde \omega=A_l\mathrm{d} l\) , \(\oint_L A_l \mathrm{d} l = \int_{\partial N}\omega\)

5.4 体元 #

考虑有度规 \(g_{ab}\) 的二维定向流形。 \(\epsilon_{a_1a_2}\) 为一体元，则 \(\epsilon^{a_1a_2}\equiv g^{a_1b_1}g^{a_2b_3}\epsilon_{b_1b_2}\) 有意义，且缩并 \(\epsilon^{a_1a_2}\epsilon_{a_1a_2}\) 为标量场，可借助任意基底计算。我们选定正交归一基底计算，考虑度规为正定/洛伦兹的情况。(2-form \(\epsilon_{ab}\) 满足： \(\epsilon_{12}=-\epsilon_{21},\epsilon_{ii}=0\) )

1. \(g_{ab}\) 正定，则 \[\epsilon^{a_1a_2}\epsilon_{a_1a_2}=\delta_{\mu_1\nu_1}\delta_{\mu_2\nu_2}\epsilon_{\nu_1\nu_2}\epsilon_{\mu_1\mu_2}=\delta_{11}\delta_{22}\epsilon_{12}\epsilon_{12}+\delta_{22}\delta_{11}\epsilon_{21}\epsilon_{21}=2(\epsilon_{12})^2\]
2. \(g_{ab}\) 洛伦兹，得到： \[\epsilon^{a_1a_2}\epsilon_{a_1a_2}=-2(\epsilon_{12})^2\]

推广到任意度规的 \(n\) 维流形： \[\epsilon^{a_1\cdots a_n}\epsilon_{a_1\cdots a_n} = (-1)^s n!(\epsilon_{1\cdots n})^2\] ,其中 \(s\) 为 \(g_{ab}\) 在正交归一基底分量中 \(-1\) 个数。利用度规可选择该值为 \(\pm 1\) ，即： \[\epsilon_{1\cdots n} = \pm 1\\ \epsilon_{a_1\cdots a_n} = \pm (e^1)_{a_1}\wedge \cdots \wedge (e^n)_{a_n}\qquad(正交归一基矢下)\] 即相当于要求 \(\epsilon^{a_1\cdots a_n}\epsilon_{a_1\cdots a_n}=(-)^sn!\) 。此即与度规 \(g_{ab}\) 相适配的体元.加上"体元与定向相容"的条件后，可唯一确定体元。 在 \(\mathbb{R}^3\) 上， \(\epsilon=\mathrm{d} x\wedge \mathrm{d} y\wedge \mathrm{d} z\) 为定向，也是笛卡尔系的适配体元。另一方面，由流形上积分的定义， \(\int_G\epsilon = \iiint_G\mathrm{d} x\mathrm{d} y\mathrm{d} z\) 正是空间G的体积。推广到任意带正定度规 \(g_{ab}\) 的定向流形N，若 \(\epsilon\) 为适配体元，且 \(\int_N\epsilon\) 存在，则称它为N的体积。

上面的定理十分重要，证明请见书中P117，此处略去。

下面证明两个关于体元的等式。为此先给出一个引理：

5.5 函数在流形上的积分，Gauss定理 #

由定义知，函数积分和体元选择有关。约定只要给定度规，就用适配体元定义函数积分。 以 \(\mathbb{R}^3,\delta_{ab}\) 为例，设 \(\{x,y,z\}\) 为右手笛卡尔系，则 \(\epsilon=\mathrm{d} x\wedge \mathrm{d} y\wedge \mathrm{d} z\) 是适配体元，于是 \(\mathbb{R}^3,\delta_{ab}\) 上的函数 \(f:\mathbb{R}^3\to\mathbb{R}\) 的积分为： \[\int f=\int f\epsilon = \int \omega=\iiint F(x,y,z)\mathrm{d} x\mathrm{d} y\mathrm{d} z\] 其中 \(\omega = F(x,y,z)\mathrm{d} x\wedge \mathrm{d} y\wedge \mathrm{d} z\) 也可以使用球坐标系 \(r,\theta,\phi\) 计算。由 \[\mathrm{d} s^2 = \mathrm{d} r^2 + \mathrm{d} \theta^2+r^2\sin^2\theta\mathrm{d} \phi^2\] 可知 \(g=\det{g_{\mu\nu}}=r^4\sin^2\theta\) , \(\epsilon = r^2\sin\theta\mathrm{d} r\wedge \mathrm{d} \theta\wedge \mathrm{d} \phi\) ，于是 \(\omega= f\epsilon =\hat F(r,\theta,\phi)r^2\sin\theta\mathrm{d} r\wedge\mathrm{d} \theta \wedge \mathrm{d} \phi\) , \[\int f = \int f\epsilon = \int\omega = \iiint \hat{F}(r,\theta,\phi) r^2\sin \theta\mathrm{d} r\mathrm{d} \theta \mathrm{d} \phi\] 推广高斯定理，得到：

进行进一步改写。我们首先得到 \(\partial N\) 的体元。当 \(\partial N\) 不是类光超曲面时， \(\partial N\) 存在归一化法矢 \(n^a\) ，满足 \(n^an_a=\pm 1\) ，于是N上度规 \(g_{ab}\) 在其上诱导度规为 \(h_{ab}=g_{ab}\mp n_an_b\) 。把 \(\partial N\) 看作带度规的 \(n-1\) 维流形，其体元应与 \(\partial N\) 的诱导定向相容，且与度规 \(h_{ab}\) 适配：即 \[\hat \epsilon^{a_1\cdots a_{n-1}}\hat \epsilon _{a_1\cdots a_{n-1}}=(-1)^s(n-1)!\] 其中 \(\hat s\) 是 \(h_{ab}\) 对角元中负数个数。 \(\partial N\) 上满足这两个条件的称为诱导体元。设 \(n^b\) 为 \(\partial N\) 的外向单位法矢量，则诱导体元和N上体元之间有关系： \[\hat \epsilon_{a_1\cdots a_{n-1}}=n^b \epsilon_{ba_1\cdots a_{n-1}}\]

5.6 对偶微分形式 #

以 \(\Lambda_{p}(l)\) 代表 \(p\in M\) 的全部 \(l\) 形式的集合，则可以得到l形式的维数为： \[\dim \Lambda_{p}(l) = \frac{n!}{l!(n-l)!} = \dim \Lambda_{p}(n-l)\] 若 \(M\) 为带度规 \(g_{ab}\) 的定向映射， \(\epsilon\) 为适配体元，则可以用这个体元和度规在 \(\Lambda_M(l)\) 和 \(\Lambda_{M}(n-l)\) 之间定义一个同构映射 \(*\) 如下：

对上式再取star: \[{}^*(^*f)=^*(f\epsilon)=\frac{1}{n!}f\epsilon^{b_{1}\dots b_{n}}\epsilon_{b_{1}\dots b_{n}}=(-1)^sf.\] 两次对偶后得到的并不是原形式场，而是有可能与之相差一个负号。这个正负号取值是由号差（对欧式度规， \(s=0\) ；对洛伦兹度规， \(s=1\) ）和对偶形式场的 \(l\) 决定。一般的，我们有下面的定理：

矢量代数的点乘和叉乘运算：记 \(\vec{A},\vec{B}\) 为 \(A^a,B^b\) ，则二者点乘为 \(\vec{A} \cdot \vec{B}=A_{a}B^a\) 。对于 \(\vec{A}\times \vec{B}\) 该如何理解？ 令 \(\omega_{ab} = A_{a}\wedge B_{b}=2A_{[a}B_{b]}\) ，则 \[{}^*\omega_{c} = \frac{1}{2}\omega^{ab}\epsilon_{abc} = \epsilon_{abc}A^{[a}B^{b]} = \epsilon_{abc}A^{[a}B^{b]}\] 其中 \(\epsilon_{abc}\) 为欧式度规的适配体元。设 \(\{x,y,z\}\) 为右手笛卡尔坐标系，则坐标基底正交归一，于是 \(\epsilon_{abc}\) 在此系得非零分量 \(\epsilon_{ijk}\) 为： \[\epsilon_{123}=\epsilon_{312}=\epsilon_{231}=1,\epsilon_{132}=\epsilon_{321}=\epsilon_{213}=-1\] 于是 \(\epsilon_{ijk}\) 就是熟知得Levi-Civita符号。于是 \({}^*\omega_{c}\) 在该笛卡尔系得第k分量为： \[{}^*\omega_{k}=\epsilon_{ijk}A^iB^j,\tag*{k=1,2,3}\] 可见，对 \(\vec{A},\vec{B}\) 求叉乘就是先求 \(A\wedge B\) 再求其对偶形式，可表示为 \(\times=*\circ \wedge\) 利用Hodge star和微分算符 \(\mathrm{d}\) ，可以表示三维矢量分析中的散度、梯度和旋度：

同时，利用“ \(\mathbb{R}^3\) 上闭形式必恰当”，我们很容易证明无旋矢量场必有标量势，无散矢量场必有矢量势： \[\begin{aligned} \text{curl}\ \vec{E}=0&\implies{}^*\mathrm{d}E=0,\mathrm{d}E=0 \\ &\implies\exists \omega\ \text{such that}\ E=\mathrm{d}\omega \\ &\implies \exists \phi\ \text{such that}\ \vec{E}=\text{grad} \phi\\ \end{aligned}\]