chap4:Lie derivatives, Killing fields, hypersurfaces #
4.1 流形间的映射 #
设 \(M,N\) 为流形, \(\phi:M\to N\) 为光滑映射, \(\mathscr F_M\) 和 \(\mathscr F_N\) 分别为M和N上光滑函数的集合, \(\mathscr F_M(k,l),\mathscr F_N(k,l)\) 分别为M和N上光滑张量场集合,由 \(\phi\) 自然诱导出一系列映射:
\(\phi^*:\mathscr F_N\to\mathscr F_M\) 定义为: \[(\phi^*f)|_p :=f|_{\phi(p)},\forall f\in\mathscr F_N,p\in M\] 或者写成: \((\phi^*f)(p)=f(\phi(p))\)
- 线性
- \(\phi^*(fg)=\phi^*(f)\phi^*(g)\)
\(\phi_*:V_p\to V_{\phi(p)}\) 定义为: \[(\phi_*v)(f):=v(\phi^*f),\forall f\in\mathscr F_N\]
\(\phi_*\) 是线性映射: \(\phi_*(\alpha u^a+\beta v^a) = \alpha\phi_*u^a+\beta\phi_* v^a\)
拉回映射可延拓至 \(\phi^*:\mathscr F_N(0,l)\to \mathscr F_M(0,l)\) :对任意 \(T\in\mathscr F_N(0,l)\) ,定义 \(\phi^*T\in \mathscr F_M(0,l)\) 为: \[(\phi^*T)_{a_1\cdots a_l}|_p (v_1)^{a_1}\cdots (v_l)^{a_l}:= T_{a_1\cdots a_l}|_{\phi(p)} (\phi_*v_1)^{a_1}\cdots (\phi_*v_l)^{a_l},\forall p\in M,v_1\cdots v_l\in V_p\]
推前映射 \(\phi_*\) 可按如下方式延拓为 \(p\) 到 \(\phi(p)\) 张量空间的映射: \(\phi_*:\mathscr T_{V_p}(k,0)\to \mathscr T_{V_{\phi(p)}}(k,0)\) : \[(\phi_* T)^{a_1\cdots a_k}(\omega^1)_{a_1}\cdots(\omega^k)_{a_k}:=T^{a_1\cdots a_k}(\phi^*\omega^1)_{a_1}\cdots (\phi^*\omega^k)_{a_k},\\ \forall \omega^1\cdots\omega^k \in V^* _{\phi(p)},T\in\mathscr T_{V_p}(k,0)\] 其中 \(\phi^*\omega_a\) 定义为 \((\phi^*\omega)_av^a\equiv \omega_a(\phi_*v)^a\)
拉回映射的延拓是拉回映射 \(k=1\) 时的特例,拉回映射是把N上的 \((0,l)\) 型张量场变成M上同类型张量场,是场之间的变换; 推前映射的延拓是推前映射 \(l=0\) 时的特例,推前映射是把 \(p\) 点 \((k,0)\) 型张量变为像点 \(\phi(p)\) 点的同型张量,但不能变成场和场之间的映射,因为对N上任意一个点 \(q\) ,M中不一定存在它的原像 \(p=\phi^{-1}(q)\) ,因此张量场在 \(q\) 处的值就无法定义。
但如果映射是一个微分同胚(一一到上,且正逆映射均为 \(C^\infty\) ),则推前映射可以改为 \((k,0)\) 型张量场之间的映射。因为逆映射 \(\phi^{-1}\) 也是微分同胚,因此也有pull back/push forward,而逆映射的pull back正是正映射的push forward,即 \(\phi^{-1 *}:\mathscr F_M(0,l)\to\mathscr F_N(0,l)\) 。因此可以进一步将推前映射 \(\phi_*\) 推广为 \(\phi_*:\mathscr F_M(k,l)\to\mathscr F_N (k,l)\) .例如,对 \((1,1)\) 型张量而言, \[(\phi_*T)^a{}_b|_q \omega_av^b \equiv T^a{}_b|_{\phi^{-1}(q)}(\phi^*\omega)_a(\phi^*v)^b,\qquad \forall q\in N,\omega_a\in V_q^*,v^b \in V_q\]
其中
\((\phi^*v)^b\)
应理解为
\((\phi_*^{-1}v)^b\)
考虑
\(M,N\)
之间存在微分同胚
\(\phi\)
,将
\(p\)
映射到
\(\phi(p)\)
。设在含p区域
\(O_1\)
中有坐标
\(\{x^\mu\}\)
,含
\(\phi(p)\)
的区域有坐标
\(\{y^\mu\}\)
,从而可以在M中的
\(\phi^{-1}[O_2]\)
中定义坐标
\(x'^\mu\)
为:
\(x'^\mu(p)\equiv y^\mu(\phi(p))\)
,如右图所示。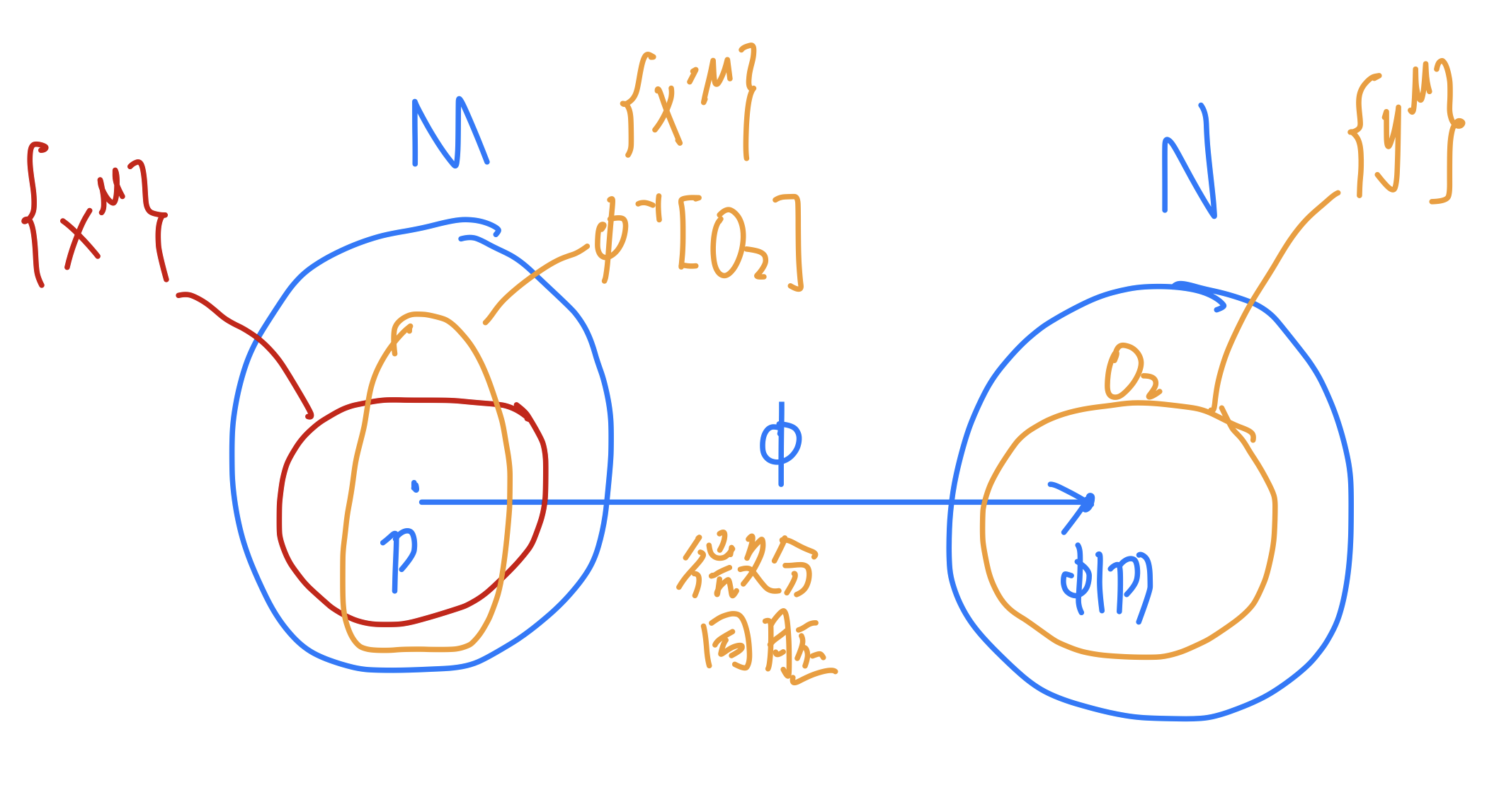 在M中
\(O_1\cap \phi^{-1}[O_2]\)
的区域中有坐标变换:
\(\{x^\mu\}\to\{x'^\mu\}\)
有两种看待微分同胚的观点:
在M中
\(O_1\cap \phi^{-1}[O_2]\)
的区域中有坐标变换:
\(\{x^\mu\}\to\{x'^\mu\}\)
有两种看待微分同胚的观点:
- 主动观点:把 \(p\) 变为 \(\phi(p)\)
- 被动观点:把 \(\phi\) 看成坐标变换 \(\{x^\mu\}\to\{x'^\mu\}\)
Claim: \((\phi_*T)^\mu{}_{\nu}|_{\phi(p)}=T'^\mu{}_{\nu}|_p\) , \(T'\) 代表用坐标系 \(\{x'^\mu\}\) 表示下的分量 上式左边是新点 \(\phi(p)\) 、新张量 \(\phi_*T\) 在老坐标系 \(\{y^\mu\}\) 下分量,右边是老点 \(p\) 、老张量 \(T\) 在新坐标系 \(\{x'^\mu\}\) 下分量。
对于微分同胚
\(\phi\)
,曲线
\(C(t)\)
即其上一点p,有曲线的像
\(\phi(C(t))\)
和像点
\(\phi(p)\)
,该点切矢
\(v\)
的像
\(\phi_*(v)\)
正是新的曲线的切矢,即"曲线的像的切矢=曲线的切矢的像",如图所示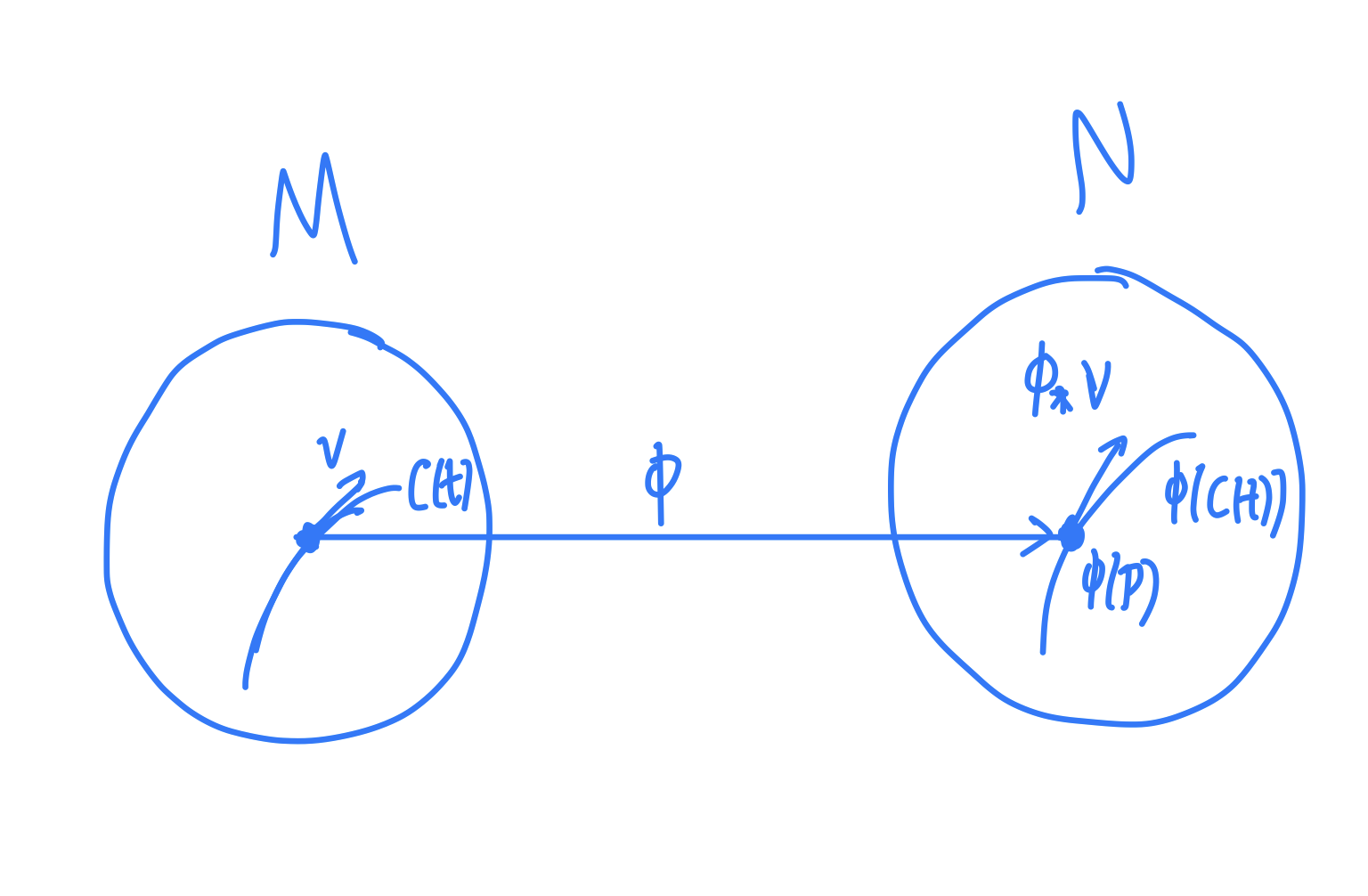
对于坐标线的坐标基矢,就有: \[\phi_*[\left({\partial \over\partial x'^\mu } \right)^a\mid_p]=\left({\partial \over\partial y^\mu } \right)^a\mid_{\phi(p)}\\ \phi_*[(dx'^\mu)_a|_p]= (dy^\mu)_a|_{\phi(p)}\]
4.2 李导数 #
2.2曾提到, \(M\) 上的光滑矢量场 \(v^a\) 给出一个单参微分同胚群 \(\phi:\mathbb{R} \times M\to M\) ,用它可以定义一个张量场的Lie导数:
\[\mathscr L_v T^{a_1\cdots a_k}{}_{b_1\cdots b_l} \equiv \lim_{t\to 0} \frac 1 t (\phi_t^* T^{a_1\cdots a_k}{}_{b_1\cdots b_l}-T^{a_1\cdots a_k}{}_{b_1\cdots b_l})\] 称为张量场 \(T^{a_1\cdots a_k}{}_{b_1\cdots b_l}\) 沿矢量场 \(v^a\) 的李导数(Lie derivative)
\(\phi_t^*\) 为线性映射,因此李导数是 \(\mathscr F_{M}(k,l)\) 到自身的线性映射。
任意 \(p\in M\) ,设 \(C(t)\) 是 \(\phi\) 过 \(p\) 的轨道, \(p=C(0)\) ,则 \(\phi_t(p)=C(t)\) ,且 \(v^a|_p \equiv ({\partial \over\partial t} )^a|_p\) 是 \(C(t)\) 在p点切矢,故 \[\begin{aligned} \mathscr L_v f|_p &= \lim_{t\to 0}\frac 1 t (\phi_t^*f-f)|_p=\lim_{ t\to 0}\frac 1 t [f(\phi_t(p))-f(p)]\\ &= \lim_{t\to 0}\frac 1 t[f(C(t))-f(C(0))] = {\mathrm d\over \mathrm dt}(f\circ C)|_{t=0}=v(f)|_p \end{aligned}\]
下面介绍一种对计算李导数很有用的坐标系。对于 \(\{x^1,x^2\}\) 组成的网格,要确定坐标域中点的坐标,只需要确定它位于哪两条坐标线交点。求李导数要给定矢量场 \(v^a\) ,可选定它的积分曲线为 \(x^1\) 坐标线( \(t=x^1\) ),再随意选定不平行的切矢作为 \(x^2\) 坐标线,得到的坐标系称为矢量场 \(v^a\) 的适配坐标系。换句话说,就是 \(v^a=(\partial/\partial x^1)^a\) .定义可以向高维推广。
张量场 \(T^{a_1\cdots a_k}{}_{b_1\cdots b_l}\) 沿 \(v^a\) 的李导数在其适配坐标系分量为 \[(\mathscr L_v T)^{\mu_1\cdots \mu_k}{}_{\nu_1\cdots \nu_l}={\partial T^{\mu_1\cdots \mu_k}{}_{\nu_1\cdots \nu_l}\over\partial x^1}\]
仅以 \(n=2,k=l=1\) 为例,由 \[\phi_t^* = (\phi_t^{-1})_*=\phi_{-t*},\] 在任意适配坐标系的分量式为: \[(\mathscr L_vT)^\mu{}_\nu |_p = \lim_{t\to 0} \frac 1 t [(\phi_{-t*}T)^\mu{}_\nu |_p-T^\mu{}_\nu|_p],\qquad \forall p\in M\] 令 \(q\equiv \phi_t(p)\) ,因为p和q相距很近,可认为在同一坐标域内。对 \(\phi_{-t}\) 而言, \(q\) 为老点,“新点 \(p\) 新张量 \(\phi_{-t*}\) 在老坐标 \(x^\mu\) 分量=老点 \(q\) 老张量 \(T\) 在新坐标 \(x'^\mu\) 分量”得到 \[(\phi_{-t*}T)^\mu{}_\nu |_p = T'^\mu{}_\nu|_q = \left[{\partial x'^\mu \over\partial x^\rho } {\partial x^\sigma \over\partial x'^\nu } T^\rho{}_\sigma\right]_q\] 新坐标通过 \(x'^\mu(p)\equiv y^\mu(\phi(p))\) 由新老坐标系的变换 \(\phi_{-t}\) 决定。取 \(\bar p\) 和 \(\bar q=\phi_t(\bar p)\) ,由适配坐标定义, \(x^1(\bar q)=x^1(\bar p)+t,x^2(\bar q)=x^2(\bar p)\) 。 \[x'^1(\bar q)\equiv x^1(\bar p)=x^1(\bar q)-t\\ x'^2(\bar q)\equiv x^2(\bar p)=x^2(\bar q)\] 即 \(x'^1=x^1-t,x'^2=x^2,\cdots\) 于是得出所有偏导数均为 \(\delta^\mu_\nu\) : \[(\phi_{-t*}T)^\mu{}_\nu |_p = T'^\mu{}_\nu|_q = \left[{\partial x'^\mu \over\partial x^\rho } {\partial x^\sigma \over\partial x'^\nu } T^\rho{}_\sigma\right]_q=T^\mu{}_\nu|_q\] 于是 \((\mathscr L_vT)^\mu{}_\nu |_p = {\partial T^\mu{}_\nu \over\partial x^1} |_p\)
使用适配坐标系: \[\begin{aligned} [v,u]^\mu& =(\mathrm{d} x^\mu)_a[v,u]^a = (\mathrm{d} x^\mu)_a(v^b\partial_bu^a-u_b\partial_bv^a) \xlongequal{v^a=({\partial \over\partial x^1} )^a}v^b\partial_b u^\mu\\ &\xlongequal{(4)} v(u^\mu)={\partial u^\mu \over\partial x^1} =(\mathscr L_v u)^\mu \end{aligned}\]
4.3 Killing 矢量场 #
李导数的定义不要求流形M有附加结构。但若选定了度规场 \(g_{ab}\) ,则对微分同胚映射 \(\phi:M\to M\) 可以提出更高要求: \(\phi^*g_{ab}=g_{ab}\)
微分同胚 \(\phi:M\to M\) 称为等度规映射,简称等度规,若 \(\phi^*g_{ab}=g_{ab}\)
M上有一类矢量场,为光滑矢量场。我们已经知道,每个光滑矢量场给出一个单参微分同胚群。如果M上指定了度规场 \(g_{ab}\) ,则众多光滑矢量场中还可挑出一部分,它们给出的单参微分同胚群是单参等度规群。
\((M,g_{ab})\) 上的矢量场 \(\xi^a\) 称为Killing矢量场,若它给出的单参微分同胚群是单参等度规群。 \(\xi^a\) is Killing 等价于 \(\mathscr L_{\xi}g_{ab}\equiv\lim_{t\to 0}(\phi_t^* g_{ab}-g_{ab})=\lim_{t\to 0}(g_{ab}-g_{ab})=0\)
\(\xi^a\) 为Killing矢量场的充要条件有:
- \(\mathscr L_{\xi}g_{ab}=0\)
- \(\nabla_a\xi_b+\nabla_b\xi_a=0\)
- \(\nabla_{(a}\xi_{b)}=0\)
- \(\nabla_a\xi_b=\nabla_{[a}\xi_{b]}\)
证明1和2等价: \[0=\mathscr L_{\xi}g_{ab} = \xi^c\nabla_cg_{ab} +g_{cb} \nabla_b\xi^c+g_{ac}\nabla_b\xi^c\\\] 选一个 \(\nabla_a\) 使得 \(\nabla_cg_{ab}=0\) ,于是 \(g_{ab}\) 可任意进出导数算符,作用在 \(\xi^c\) 上: \[0=\mathscr L_\xi g_{ab}=\nabla_a\xi_b+\nabla_b\xi_a\] 定理3和4容易从中得到
若存在坐标系 \(\{x^\mu\}\) 使得度规 \(g_{ab}\) 全部分量满足 \({\partial g_{\mu\nu}\over\partial x^1} =0\) ,则 \(({\partial \over\partial x^1} )^a\) 是坐标域上的Killing矢量场
\(\{x^1\}\) 是 \(({\partial \over\partial x^1}) ^a\) 的适配坐标系,于是有: \[(\mathscr L_{{\partial \over\partial x^1} }g)_{\mu\nu}={\partial g_{\mu\nu }\over\partial x^1} =0\]
设 \(\xi^a\) 为Killing 矢量场, \(T^a\) 为一条测地线切矢,则 \(T^a\nabla_a(T^b\xi_b)=0\) ,即内积 \(T^b\xi_b\) 沿测地线为常数。
\[T^b\nabla_b(\xi_aT^a)=\xi_aT^b\nabla_bT^a + T^aT^b\nabla_a\xi_b=T^bT^a\nabla_a\xi_b=0\] 其中第二步是因为异种括弧缩并为0: \(T^bT^a\nabla_a\xi_b=T^{(b}T^{a)}\nabla_{[a}\xi_{b]}=0\)
若 \(\xi^a,\eta^a\) 为Killing矢量场,则它们的线性组合与对易子都是Killing矢量场。
\((M,g_{ab})\) 上有最多 \(n(n+1)/2\) 个独立的Killing矢量场( \(n=\dim M\) ),即M上所有Killing矢量场的几何的维数都小于 \(n(n+1)/2\)
一般而言求Killing矢量场需要求解偏微分方程,但在一些情况下可以简化。下面举欧式空间与伪欧空间的例子:
\((\mathbb{R}^2,\delta_{ab})\) 中, \(g_{xx}=g_{yy}=1,g_{xy}=g_{yx}=0\) ,于是由4-3-2得 \(({\partial \over\partial x})^a ,{\partial \over\partial y}\) 都是Killing vector field,d代表平移对称性。 第三个: \(\mathrm{d} s^2 =\mathrm{d} r^2+r^2\mathrm{d} \varphi^2\) ,于是 \(({\partial \over\partial \varphi})^a\) 也为Killing vector field ,代表旋转对称性。 \(\partial/\partial \varphi\) 的积分曲线是一个个绕坐标原点的同心圆。
\((\mathbb{R}^3,\delta_{ab})\) 有6个独立Killing场,3个平移与3个旋转。旋转部分可写成: \(-y({\partial \over\partial x}) ^a+x({\partial \over\partial y} )^a,-x({\partial \over\partial z} )^a+z({\partial \over\partial x} )^a,y({\partial \over\partial z})^a-z({\partial \over\partial y} )^a\)
\((\mathbb{R}^2,\eta_{ab})\) , \(\mathrm{d} s^2=-\mathrm{d} t^2+\mathrm{d} x^2\) ,定义坐标变换 \(\{x,t\}\to \{\psi,\eta\}\) 为: \[x=\psi\ch \eta,t=\psi\sh \eta\] 则 \(\mathrm{d} s^2 = \mathrm{d} \psi^2-\psi^2\mathrm{d} \eta^2\) Killing vector field: \(({\partial \over\partial t})^a,({\partial \over\partial x} )^a,({\partial \over\partial \eta } )^a=t({\partial \over\partial x} )^a+x({\partial \over\partial t} )^a\) 是一个boost。
对 \({\partial \over\partial \eta}\) 的积分得到 \(\psi\) 为常数,于是 \(x^2-t^2 = \psi^2=\text{const}\) 积分曲线为双曲线。
对四维闵氏空间, \(n=4\) ,独立Killing场有10组,其中4组平移,3组空间分量转动,3组boost(伪转动)。
微分同胚是点的映射,这是一个主动观点,对应的被动观点是坐标变换。谈boost、Killing vector field时,我们用的是主动观点,对应的被动观点正是狭义相对论中的洛伦兹变换。
设 \(\{x,t\}\) 是二维闵氏空间 \((\mathbb{R}^2,\eta_{ab})\) 的洛伦兹坐标系, \(\phi_\lambda:\mathbb{R}^2\to\mathbb{R}^2\) 是伪转动Killing场 \(\xi^a\equiv t({\partial \over\partial x} )^a+x({\partial \over\partial t})^a\) 对应的单参等度规群的一个群元,则由 \(\phi_\lambda\) 诱导的坐标变换 \(\{x,t\}\to\{x',t'\}\) 是洛伦兹变换。
\(\xi^a\equiv ({\partial \over\partial \eta } )^a\) 的积分曲线的参数方程为 \(\mathrm{d} x^\mu(\eta)/\mathrm{d} \eta = \xi^\mu\) 。代入 \(\xi^a \equiv t({\partial \over\partial x} )^a +x({\partial \over\partial t} )^a\) , \[\frac{\mathrm{d} t(\eta)}{\mathrm{d} \eta }= x(\eta),\\ \frac{\mathrm{d} x(\eta)}{\mathrm{d} \eta } = t(\eta)\\\] 初值:设 \(C(\eta)\) 是满足 \(p=C(0)\) 的积分曲线,即 \(x(0)=x_p,t(0)=t_p\) 解得: \[x(\eta) =x_p \ch \eta+t_p\sh \eta ,\\ t(\eta) =x_p\sh \eta +t_p\ch \eta \\\] 设 \(q\equiv \phi_\lambda (p)\) ,则 \(q\) 是 \(C(\eta)\) 上参数 \(\eta = \lambda\) 的点 \(C(\lambda)\) ,则由 \(\phi_\lambda\) 诱导得到的新坐标满足: \[x_p' \equiv x_q = x_p\ch \lambda + t_p\sh\lambda,\\ t_p' \equiv t_q = x_p \sh \lambda + t_p\ch \lambda \\\] 令 \(v\equiv \tanh \lambda,\gamma \equiv (1-v^2)^{1/2}=\ch \lambda\) ,则成为物理中熟悉的洛伦兹变换: \[x'=\gamma(x+vt),\qquad t'=\gamma(t+vx)\]
设 \(\{x^\mu\}\) 是 \((\mathbb{R}^n,\eta_{ab})\) 的洛伦兹坐标系,则 \(\{x'^\mu\}\) 也是洛伦兹坐标系的充要条件为:它是由 \(\{x^\mu\}\) 通过等度规映射 \(\phi:\mathbb{R}^n\to\mathbb{R}^n\) 诱导而得。
A. 证明等度规映射诱导得到洛伦兹系: \(g'_{\mu\nu}|_p\xlongequal{老老新=新新老}(\phi_*g)_{\mu\nu}|_{\phi(p)}=(\phi^{-1*}g)_{\mu\nu}|_{\phi(p)}\xlongequal{逆映射等度规}g_{\mu\nu}|_{\phi(p)}=\eta_{\mu\nu}\)
B. 洛伦兹系之间等度规: \((\phi^{-1*}g)_{\mu\nu}|_{p}=(\phi_*g)_{\mu\nu}|_p=g'_{\mu\nu}|_{\phi^{-1}(p)}=\eta_{\mu\nu}=g_{\mu\nu}|_p\)
4.4 超曲面 #
设 \(M,S\) 为流形, \(\dim S\le \dim M \equiv n\) ,映射 \(\phi:S\to M\) 称为嵌入(imbedding),若 \(\phi\) 是一一和 \(C^\infty\) 的,且 \(\forall p\in S,\phi_*:V_{p}\to V_{\phi_p}\) 非退化,即 \(\phi_*v^a = 0\Rightarrow v^a=0\)
嵌入 \(\phi:S\to M\) 称为M的一个嵌入子流形,简称子流形(imbedded submanifold)。也常把 \(\phi [S]\) 称为子流形。若 \(\dim S=n-1\) ,则 \(\phi [S]\subset M\) 为M的一张超曲面(hypersurface)。
U是M的开子集,M的流形结构限制在U上,就构成了与M同维的子流形。令 \(\phi: U\to M\) 为恒等映射,则 \(U\equiv \phi [U]\) 为一个同维嵌入。
\(S^2\) 为二维单位球面,则 \(\phi: S^2\to \mathbb{R}^3\) 给出 \(\mathbb{R}^3\) 的嵌入子流形。这是 \(\mathbb{R}^3\) 的一个超曲面。
研究比原流形M仅低一维的子流形的优势在于,在子流形S上任意一点 \(q\) ,存在唯一一个方向的“矢量” \(\vec n\) 使得它与子流形上该点切空间中所有的矢量“正交”。但正交性只有在定义度规后才能谈及,在没有度规时,这个矢量则是对偶矢量,即“法余矢” \(n_a\)
设 \(\phi [S]\) 是超曲面, \(q\in \phi [S]\) ,非零对偶矢量 \(n_a\in V_q^*\) 称为q点法余矢(normal covector),若 \(n_aw^a=0,\forall w^a\in W_q\)
超曲面上任意一点必有法余矢,且该点全部法余矢之间只差一实因子。
设 \(\phi [S]\) 由 \(f=\text{const}\) 给出,则 \(\nabla_a f\) 给出的是超曲面的法余矢
\(\forall w^a\in W_q\) , \(W_q\) 为子流形该点切空间。 \(w^a\) 总切于超曲面上一曲线 \(C(t)\) ,故 \(w^a\nabla_a f= {\partial \over\partial t} f = 0\)
若有了度规 \(g^{ab}\) ,则可以定义法矢量 \(n^a =g^{ab}n_b\) 。对洛伦兹度规, \(n^a\) 有可能属于 \(W_q\) .
\(n^a\in W_q\) 当且仅当 \(n^an_a = 0\)
若 \(n^a\in W_q\) , \(n_aw^a=0,n_an^a=0\) 由 \(n^an_a=0\) ,对任意一个法余矢 \(n_a\) ,存在基底 \(\{(e_\mu)^a\}\) 使得 \(n_a=(e^1)_a,(e_k)^a\in W_q,k\ge 2\) .故 \(n^1=n^a(e^1)_a=0\) , \(n^a=\sum_{p=2}^nn^p(e_p)^a\in W_q\)
超曲面是类空的,若法矢量处处类时( \(n^an_a<0\) );超曲面是类时的,若法矢量处处类空( \(n^an_a>0\) );超曲面是类光的(null),若法矢量处处类光( \(n^an_a= 0\) ).
若法矢量不是类光的,以后都对法矢量进行归一化( \(n^an_a=\pm 1\) )
设 \(\phi [S]\) 是流形M上的嵌入子流形, \(q\in \phi [S]\) , \(W_q\) 是q点切于 \(\phi [S]\) 的切空间。 \(W_q\) 度规 \(h_{ab}\) 叫做 \(V_q\) 的度规 \(g_{ab}\) 生出的诱导度规(induced metric),若 \[h_{ab}w_1^aw_2^b = g_{ab}w_1^aw_2^b,\qquad \forall w_1^a,w_2^b \in W_q\]
\(h_{ab}\) 还可以写成: \(h_{ab}=g_{ab}\mp n_an_b\) ,其中 \(n_a,n_b\) 是单位法余矢。代入,根据正交性即可得到。
考虑曲面是类光超曲面的情形:记 \(W_q\) 为面上一点在面内的切空间,此时法矢量 \(n^a\in W_q\) . 如果设 \(h_{ab}\) 是诱导得到的度规, \(\forall w^b\in W_q\) , \(h_{ab}n^aw^b=g_{ab}n^aw^b=0\) 。由度规的性质(对称,非退化),应有 \(g(v,u)=0,\forall u\in W_q\qquad \Rightarrow v=0\) 法矢量 \(n^a\) 在切空间内,且与 \(W_q\) 中任意矢量内积为0,但它自身不是0。因此 \(h_{ab}\) 是退化的,不能充当度规。故类光超曲面没有诱导度规。
对于非类光超曲面的情形,利用度规可以对 \(h_{cb}\) 进行指标升降: \(h^a{}_b\equiv g^{ac}h_{cb}=g^{ac}(g_{cb}\mp n_cn_b)= \delta^a{}_b \mp n^an_b\) 于是我们得到,对任意矢量 \(v^a\) ,有: \[h^a{}_b v^b = v^a \mp n^a (n_b v^b)\\ v^a\equiv h^a{}_b v^b \pm n^a(n_bv^b)\] 上式正是对 \(v^a\) 的一个分解。可以证明, \(h^a{}_bv^b\) 没有法向分量: \(n_ah^a{}_b=n_a(\delta^a{}_b\mp n^an_b)=n_b\mp (\pm 1 n_b)=n_b-n_b = 0\)
\(h^a{}_bv^b\) 事实上是向量 \(v^a\) 在超曲面上的投影。