2.1 微分流形 #
拓扑空间 \((M,\mathscr T)\) 称为n维微分流形(n-dimensional differentiable manifold),若 \(M\) 有开覆盖 \(\{O_\alpha\}\) 满足: a. \(\forall O_\alpha ,\exists 同胚\Psi_\alpha:O_\alpha\to V_\alpha\) ( \(V_\alpha\) 为 \(\mathbb{R}^n\) 用通常拓扑衡量的开子集); b. \(\text{if}\ O_\alpha \cap O_\beta \ne \emptyset\) ,复合映射 \(\Psi_\beta\circ \Psi_\alpha^{-1}\) 是 \(C^\infty\) 光滑的。
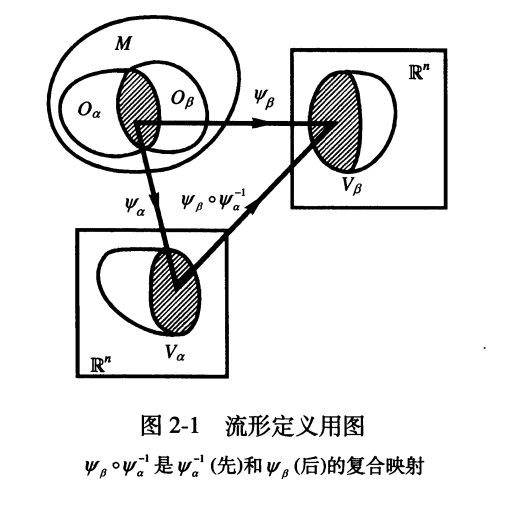
\(\psi_\beta \circ \psi_\alpha^{-1}\) 是 \(\mathbb{R}^n\) 的子集之间的映射,每个点都有n个自然坐标。因此它提供了n个n原函数。 \(C^\infty\) 表示每个n元函数都是无穷阶光滑的。尽管原来的拓扑空间没有坐标,但其中的开覆盖有了和 \(\mathbb{R}^n\) 的同胚之后就可以用 \(\mathbb{R}^n\) 的坐标去定义其中点的坐标。每个开覆盖对应的同胚不同,因此两个覆盖的交集就有了两套坐标 \(\{x^\mu\},\{x^\nu\}\) ,映射 \(\psi_\beta\circ\psi_\alpha^{-1}\) 提供的就是二者的一个坐标变换。
\(C^\infty\) 光滑对应的流形为光滑流形,类似还可定义 \(C^r\) 流形、解析流形
\((O_\alpha,\psi_\alpha)\) 称作图(chart),满足定义1的 \(\{(O_\alpha,\psi_\alpha)\}\) 为图册,条件b又称作相容性条件。
例1:容易知道 \(\mathbb{R}^n,\mathscr T_u\) 是平凡流形。
\(M=(S^1,\mathscr S)\) ,其中 \(S^1\) 并不与 \(\mathbb{R}\) 同胚,因此要取至少两个图,才能证明其为流形。
\(M=(S^2,\mathscr T)\) 是微分流形。 \(\mathscr T\) 是 \(\mathbb{R}^3\) 的 \(\mathscr T_u\) 在 \(S^2\) 上的诱导拓扑。可以用六个开半球面覆盖 \(S^2\) ,然后用它到 \(\mathbb{R}^2\) 开圆盘的同胚证明交叠区域满足相容性条件。也可以用两个图覆盖 \(S^2\)
可以用不同的图定义把同一个拓扑空间定义为一个流形,但有可能两个图 \(\{(O_\alpha,\psi_\alpha)\}\) \(\{(O_\beta',\psi_\beta)\}\) 不相容,也就是 \(O_\a和O'_\beta\) 使得二者交集非空,且交集上的映射 \(\psi_\alpha\circ\psi_\beta^{-1}\) 不满足 \(C^\infty\) ,我们称为代表不同的微分结构。
如果相同,我们可以把所有与 \((O_\alpha,\psi_\alpha)\) 相容图放在一起做出做大的图册。以后总是默认已经选定最大图册,使得我们可以任意进行坐标变换。
\(f:M\to M'\) 称为 \(C^r\) 类映射,如果 \(\forall p\in M,\) 映射 \(\psi_\beta' \circ f \circ \psi_\alpha ^{-1}\) 对应的 \(n'\) 个 \(n\) 元函数是 \(C^r\) 类的。
微分流形 \(M\) 和 \(M'\) 互相微分同胚,若 \(\exists f:M\to M'\) ,满足: a. \(f\) 为一一到上的; b. \(f,f^{-1}\) 是 \(C^\infty\) 的 这样的 \(f\) 称为从 \(M\) 到 \(M'\) 的微分同胚映射,简称微分同胚。
\(f\ :\ M \to\mathbb R\) 称为M上的函数或M上的标量场,若 \(f\) 为 \(C^\infty\) 的,则称为M上的光滑函数。M上全体光滑函数集记作 \(\mathscr F_M\)
\(\mathbb{R}^3\) 中q点的点电荷的电势是流形 \(M\equiv \mathbb R^3-\{q\}\) 上的光滑函数。
可以利用 \(M,N\) 两个流形的流形结构把 \(M\times N\) 进一步定义为流形。设M,N的尾数分别为m,n,则 \(M\times N\) 的维数为m+n。
2.2 切矢和切矢场 #
实数域上定义了加法和数乘的集合,满足线性空间的性质。略
\(\underline{0}\in V,0\in \mathbb{R}\) 二者均记作0.
任意满足定义的集合都叫做矢量空间。在三维欧式空间,从一点 \(p\) 出发的所有方向和长度的直线段集合记作 \(V_p\) ,定义相应的加法和数乘,它就成了矢量空间。 我们希望能把这种矢量概念推广到任意流形M。 设 \(\vec v\) 是 \(\mathbb{R}^3\) 中任一点p的一个箭头,则对 \(\mathbb{R}^3\) 上的任意 \(C^\infty\) 函数 \(f\) 可以沿 \(\vec v\) 求方向导数,这导函数在 \(p\) 点的值是一个实数,可见如果记 \(\mathscr F_{\mathbb{R}^3}\) 为 \(\mathbb{R}^3\) 上所有光滑函数 ,则 \(\vec v:\mathscr F_{\mathbb{R}^3}\to\mathbb{R}\) 。由于求方向导数有线性性,满足莱布尼茨律,我们找到了这样的线性映射。
映射 \(v:\mathscr F_M\to \mathbb{R}\) 称为 p点的一个矢量 ,若 \(\forall f,g\in \mathscr F_M, \alpha,\beta\in\mathbb{R}\) 有:
- 线性性: \(v(\alpha f+\beta g) = \alpha v(f)+\beta v(g)\) ;
- 莱布尼茨律: \(v (fg) = f|_p v(g) +g|_p v(f)\) ,其中 \(f|_p = f(p)\)
设 \((O,\psi)\) 是坐标系,其坐标 \(x^\mu\) , 则M上的任意光滑函数 \(f\in \mathscr F_M\) 与之结合得n元函数 \(F(x^\mu)\) ,它们作用于任一 \(f\in \mathscr F_M\) 得结果 \(X_\mu(f)\) 定义为如下实数:
\[X_\mu (f):=\left.{\partial F(x^1\cdots x^n)\over\partial x^\mu } \right|_p\] 因此 \(X_\mu : \mathscr F_M\to \mathbb{R}\) 是一组矢量。 下面将 \(F\) (微分流形对应坐标 \(\mathbb{R}^n\) 到 \(\mathbb{R}\) 的映射)简写成向量场(微分流形到R的映射) \(f\) 。
\(V_p\) 代表 \(M\) 中 \(p\) 点所有矢量集合,则 \(V_p\) 是n维矢量空间,n为M的维数。 \[\dim V_p = \dim M = n\]
-
证明 \(V_p\) 构成矢量空间。
-
上面定义了 \(p\) 点的n个矢量 \(X_\mu\) ,欲证明它们线性独立,设n个实数 \(\alpha^\mu\) 使得 \(\alpha^\mu X_\mu = 0\) ,由于坐标 \(x^\nu\) 可以看作坐标域上的函数, \(\underline{0}(x^\nu) = 0\) ,于是等号左侧为 \[\alpha^\mu X_\mu(x^\nu ) = \alpha^\mu{\partial x^\nu \over\partial x^\mu }|_p = \alpha^\nu\] 故 \(\alpha^\nu = 0\) ,线性独立。
-
再证明 \(\forall v \in V_p\) , \[v = v^\mu X_\mu , \\ v^\mu = v(x^\mu)\]
坐标域内任一点p的 \(\{X_1\cdots X_n\}\) 称为 \(V_p\) 的一个坐标基底,每个 \(X_\mu\) 称为一个坐标基矢, \(v\in V_p\) 用 \(\{X_\mu \}\) 线性标出的系数称为 \(v\) 的坐标分量。
有点晕了,总结一波 首先被作用的对象是微分流形 \(M\) 到实数的全体光滑映射, \(M\) 在一个开覆盖内同胚于一组坐标 \(\mathbb R^n\) ,所以作用对象等价于 \(\mathbb{R}^n\to \mathbb{R}\) 流形中一个点p的矢量 类似于把它们向实数映射的函数,这个函数满足线性和复合函数的求导律。这个操作看成求函数在这个方向上的导数。 这样构成了矢量空间,其中一组基矢就是向着 \(n\) 个坐标分量求偏导,并代入p点值的算符。
\(\{x^\mu\},\{x^\nu\}\) 为两个坐标系,其坐标域的交集非空,p为交集中的一点, \(v \in V_p\) , \(\{v^\nu\},\{v'^\nu\}\) 是v在这两个系的坐标分量,则 \[v'^\nu = {\partial x'^\nu \over\partial x^\mu } |_p v^\mu\] \(x'^\nu\) 是两系间坐标变换函数 \(x'^\nu(x^\sigma)\) 的简写。
两个系下的坐标基矢量为: \[X_\mu (f) = {\partial f(x)\over\partial x^\mu } |_p,\quad X_\nu' (f)={\partial f'(x')\over\partial x'^\nu } |_p\] 其中 \(f(x)=f'(x')\) , \(f\) 和 \(f'\) 分别为两个坐标下的同一个函数,x和x’为坐标。 于是 \[X_\mu (f) = {\partial f'(x'(x))\over\partial x^\mu } |_p = \left({\partial f'(x')\over\partial x'^\nu } {\partial x'^\nu \over\partial x^\mu } \right)_p={\partial x'^\nu \over\partial x^\mu } |_p X_\nu '(f)\] 对任意函数 \(f\) 成立,于是 \[X_\mu = {\partial x'^\nu \over\partial x^\mu } |_p X'_\nu\]
\(v=v^\mu X_\mu = v'^\nu X'_\nu\) 可表示成 \[v^\mu {\partial x'^\nu \over\partial x^\mu } |_p X_\nu ' = v'^\nu X_\nu'\]
I是 \(\mathbb{R}\) 的一个区间, \(C^r\) 类的曲线为映射 \(C:I\to M\) 。曲线一般指的是光滑 \(C^\infty\) 类曲线。对 \(t\in I\) ,有唯一的点 \(C(t)\in M\) 与之对应,称为曲线的参数。
尽管像重合,对应关系不同的曲线也可以是不同曲线。二者互为重参数化。即 \(\exists 一一对应\alpha:I\to I'\) ,满足 \(C=C'\circ \alpha\) ,且由 \(\alpha\) 诱导的函数 \(t'=\alpha(t)\) 有处处非零的导数。
设 \((O,\psi)\) 为坐标系, \(x^\mu\) 为坐标,则 \(O\) 的子集 \[\{p\in O|x^2(p)=\text{const},\cdots,x^n(p)=\text{const}\}\] 称为 \(x^1\) 坐标线
设 \(C(t)\) 是流形M上的 \(C^1\) 曲线,则线上 \(C(t_0)\) 点的切于 \(C(t)\) 的切矢 \(T\) 是 \(C(t_0)\) 点的矢量,它对 \(f\in \mathscr F_M\) 的作用定义为 \[T(f):=\frac{d(f\circ C)}{dt}|_{t_0},\quad \forall f\in \mathscr F_M\]
\(V_p\) 中任一元素可视为过 \(p\) 的某曲线的切矢,因此 \(p\) 点的矢量亦称切矢量, \(v\) 称为p点的切空间
2.2.2 流形上的矢量场 #
A为M的子集,若给A中每个点指定一个矢量,就得到一个定义在A上的矢量场。 \(v:M\to((M\to \mathbb{R})\to \mathbb{R})\) 矢量: \(\vec v:(M\to \mathbb{R})\to \mathbb{R}\)
非自相交曲线 \(C(t)\) 上每点的切矢构成 \(C(t)\) 上的一个矢量场。
设 \(v\) 是 \(M\) 上矢量场, \(f\) 是 \(M\) 上函数,则 \(v\) 在 \(M\) 得任一点p的值 \(v|_p\) 将按定义2把f映射为一个实数 \(v|_p(f)\) 。它在p点跑遍M时构成M上的一个函数 \(v(f):M\to \mathbb{R}\) 因此,矢量场 \(v\) 可视为把函数 \(f\) 变为函数 \(v(f)\) 的映射 \(v:(M\to \mathbb{R})\to(M\to\mathbb{R})\)
M上的矢量场 \(v\) 称为 \(C^\infty\) 光滑的,若 \(v\) 作用于 \(C^\infty\) 类函数得到的为 \(C^\infty\) 类函数,即 \(v(f)\in \mathscr F_M,\forall f\in \mathscr F_M\) ; \(v\) 为 \(C^r\) 类的,若 \(v\) 作用于 \(C^\infty\) 类函数得 \(C^r\) 类函数。
今后如无声明,矢量场均指光滑矢量场。 向 \(n\) 个坐标的偏导数构成 \(n\) 个光滑矢量场,称为坐标基矢场
两个光滑矢量场的对易子是一个光滑矢量场: \[[u,v] (f):= u(v(f))-v(u(f)),\quad \forall f\in \mathscr F_M\]
设 \(\{x^\mu\}\) 为任意坐标系,则 \([{\partial \over\partial x^\mu} ,{\partial \over\partial x^\nu} ]=0\)
\(C(t)\) 叫矢量场的积分曲线,若其上每点切矢等于该处的 \(v\) 值
设 \(v\) 是M上光滑矢量场,M的任一点p必有v的唯一积分曲线 \(C(t)\) 经过。
平移群是一个单参数群:所有群元可以用一个实数来表征。每个群元都是 \(\mathbb{R}^3\) 上的一个微分同胚,故平移群又称为 \(\mathbb{R}^3\) 上的单参微分同胚群。
\(C^\infty\) 映射 \(\phi:\mathbb{R}\times M \to M\) 称为 \(M\) 上的一个单参微分同胚群,若: (a) \(\phi_t:M\to M\) 是微分同胚, \(\forall t\in \mathbb{R}\) (b) \(\phi_t\circ\phi_s=\phi_{t+s},\forall t,s\in \mathbb{R}\)
\(\phi_0\circ \phi_t = \phi_t\) , \(\phi_0\) 是恒等映射。 设 \(\phi\) 为单参微分同胚群,则 \(\forall p\in M\) , \(\phi_p:\mathbb{R}\to M\) 是过p点的一条光滑曲线( \(\phi_p(0)=p\) ),称为单参微分同胚群过p点的轨道。记 \(v|_p=\phi_p(0)\) 处轨道曲线的切矢,便得到M上光滑向量场 \(v\) .
2.3 对偶矢量场 #
设 \(V\) 是 \(\mathbb{R}\) 上有限维矢量空间,线性映射 \(\omega:V\to\mathbb{R}\) 称为V上对偶矢量,V上全体对偶适量构成的集合为V的对偶空间,记作 \(V^*\)
定义对偶基底 \(e^{\mu*}\) : \[e^{\mu*}(e_\nu) := \delta^\mu_\nu\quad \mu,\nu = 1,\cdots,n\] \(\forall \omega\in V^*\) , \(\omega=\omega_\mu e^{\mu *}\equiv \omega(e_\mu)e^{\mu *}\)
因为 \(V\) 与 \(V^*\) 的维度相同,存在同构映射,比如 \(e_\mu \to e^{\mu *}\) ,但这样定义出来线性映射会随着基矢量的定义改变而改变。故二者之间不存在一个特殊的同构映射。 但 \(V\) 与 \(V^{**}\) 之间存在自然的同构映射: \[f:V\to V^{**}\\ v^{**}=f(v)\quad \text{such that}\quad v^{**}(\omega)=\omega(v),\forall \omega \in V^{*}\]
\(V\) 中有基底变换 \(e_\mu'=A^\nu\ _\mu e_\nu\) ,以 \(A^\nu_\mu\) 为元素拍成的非退化仿真记作A,于是相应对偶基底变换为: \[e^{'\mu *} = (\tilde{A}^{-1})_\nu\ ^\mu e^{\nu *}\]
设 \(f\in \mathscr F_M\) ,可以用f来自然诱导出 \(M\) 上的对偶矢量场 \(\mathrm df\) : \[\mathrm df|_p(v) = v(f),\quad \forall v\in V_p\] 于是,在p点有: \[\mathrm dx^\mu \left({\partial \over\partial x^\nu } \right)={\partial \over\partial x^\nu } (x^\mu ) = \delta_\nu^\mu\] \((O,\psi)\) 为一坐标系, \(\{\mathrm dx^\mu \}\) 是与坐标基底 \(\{{\partial \over\partial x^\nu } \}\) 对应的对偶坐标基底。O上的任意对偶基矢场可以以展开: \(\omega = \omega_\mu \mathrm dx^\mu\qquad \omega_\mu = \omega({\partial \over\partial x^\mu } )\)
设 \((O,\psi)\) 是一坐标系, \(f\) 是O上光滑函数, \(f(x)\) 是 \(f\circ \psi^{-1}\) 对应的 \(n\) 元函数 \(f(x^1,\cdots,x^n)\) 的简写,则 \(\mathrm df\) 可以用对偶坐标基矢 \(\{\mathrm dx^\mu\}\) 展开: \[\mathrm df = {\partial f(x)\over\partial x^\mu} \mathrm dx^\mu ,\qquad \forall f\in \mathscr F_O\]
设坐标系 \(\{x^\mu\},\{x'^\nu\}\) 的坐标域有交,则交域中任一点p的对偶矢量 \(\omega\) 在坐标系中的分量 \(\omega_\mu\) 和 \(\omega_\nu'\) 的变换关系为: \[\omega_\nu' = {\partial x^\mu \over\partial x^{\prime\nu}}|_p\omega_\mu\]
2.4 张量场 #
\[T:\underbrace{V^*\times \cdots\times V^*}_{\text{k个}}\times \underbrace{V\times\cdots\times V}_{\text{l个}}\to \mathbb R\] 张量 \(T\) 是一个多重线性映射
张量积: \((k,l)\) 型张量 \(T\) 和 \((k',l')\) 型张量 \(T'\) 的张量积 \(T\otimes T'\) 是 \((k'+k,l'+l)\) 型张量,新的张量分别合并二者的上标和下标列表。传入 \(k+k'+l+l'\) 个矢量后,首先代入T和T’,再将二者做乘积作为二者张量积的结果。
\(T\in \mathscr T_V(k,l)\) 的第i上标和第j下标( \(i\le k,j\le l\) )的收缩(contraction) \(C^i_jT\) 定义为: \[C_i^j T = \sum_\mu T(\cdot,\cdot,\cdots,e^{\mu *},\cdots;\cdot,\cdot,\cdots,e_{\mu},\cdots)\] 其中 \(e^{\mu *}\) 被塞在了第i上标位置, \(e_{\mu}\) 被塞在第j下标位置,求和号可以省略。
(2,1)型张量 \(T(\cdot,\cdot;\cdot)\) 有两种可能的缩并方式: \(C_1^1\) 与 \(C_1^2\) ,作用在T上分别得到: \[C_1^1T = T(e^{\mu *},\cdot;e_{\mu})\\ C_1^2T = T(\cdot,e^{\mu *};e_{\mu})\\\]
张量对矢量的作用可以看作先求张量积再做缩并的运算。
从流形角度:若选坐标系 \(\{x^\mu \}\) 使坐标域含 \(p\) ,可以用坐标基矢 \({\partial \over\partial x^\mu }\) 和对偶坐标基矢 \(\mathrm dx^\mu\) 充当 \(e_\mu\) 和 \(e^{\mu*}\) \[T=T^{\mu \nu}{}_\sigma {\partial \over\partial x^\mu } \otimes {\partial \over\partial x^\nu } \otimes\mathrm dx^\sigma\]
其中坐标分量 \(T^{\mu\nu}_\sigma\) 可表为 \[T^{\mu\nu}{}_\sigma =T(\mathrm dx^\mu ,\mathrm dx^\nu;{\partial \over\partial x^\sigma} )\] 若在流形M上每点都指定一个(k,l)型张量,就得到一个M上的张量场。M上张量场称为光滑的,若 \(\forall\) 光滑对偶矢量场 \(\omega^1,\omega^2,\cdots,\omega^k\) 以及光滑矢量场 \(v_1,\cdots,v_l\) ,有 \(T(\omega^1,\cdots,\omega^k;v_1,\cdots,v_l)\in \mathscr F_M\) (M上的光滑函数)。张量场如无特殊声明都指光滑( \(C^\infty\) )向量场。
2.5 度规张量场 #
矢量空间 \(V\) 上的度规 \(g\) 是V上的对称、非退化的 \((0,2)\) 型张量。 对称: \(g(v,u)=g(u,v),\forall v,u\in V\) , 非退化: \(g(v,u)=0,\forall u\in V\Rightarrow v=0\in V\)
\(v\in V\) 的长度/大小定义为: \(|v|:=\sqrt{|g(v,v)|}\) . 矢量 \(v,u\in V\) 是相互正交的,若 \(g(v,u)=0\) . 基底 \(\{e_\mu\}\) 为正交归一的,若 \(g(e_\mu,e_\nu)=g_{\mu\nu}=\pm \delta_{\mu\nu}\)
在正交归一基底下对角化后,对角元全1的度规为正定,全-1为负定,其余为不定的,只有一个-1叫洛伦兹的(Lorentzian),度规的trace为号差。
对矢量 \(v\) ,有: \[\begin{cases} g(v,v)>0, & 类空\\ g(v,v)=0, & 类光\\ g(v,v)<0, & 类时\\ \end{cases}\]
M上对称、处处非退化的(0,2)型张量场称为度规张量场
有了度规,我们可以定义曲线长度。在有正定度规场 \(g\) 的任意流形 \(M\) 上, \(C(t)\) 是 \(M\) 上任一 \(C^1\) 曲线, \(T={\partial \over\partial t}\) 是其切矢,则 \(|T|=\sqrt{g(T,T)}\) ,故 \(C(t)\) 的线长可定义为: \[l:=\int \sqrt{g(T,T)}\mathrm dt,\quad T\equiv{\partial \over\partial t}\] 若曲线在每点切矢量都类时/类空/类光,则该曲线定义为类时/类空/类光曲线。对于不同类型曲线“拼接”成的曲线,线长没有定义。
在洛伦兹度规场 \(g\) 的流形 \(M\) 上, \(l\) 不再为非负实数。此时可对 \(C(t)\) 分类:若曲线 \(C(t)\) 上每点切矢都类空 线长与坐标系选取无关,但可用特定坐标系 \(\{x^\mu\}\) 来计算:
\begin{aligned} g(T,T) &= g(T^\mu{\partial \over\partial x^\mu} ,T^\nu{\partial \over\partial x^\nu } ) \ &= T^\mu T^\nu g({\partial \over\partial x^\mu },{\partial \over\partial x^\nu } )\ &= {\mathrm dx^\mu \over \mathrm dt}{\mathrm dx^\nu \over \mathrm dt }g_{\mu\nu} \end{aligned}
最后一步用到定理2.2.4: \(T^\mu = {\mathrm dx^\mu \over \mathrm dt}\) 曲线长 \(\mathrm dl = \sqrt{|g_{\mu\nu}\mathrm dx^\mu \mathrm dx^\nu|}\) 下面给出欧式空间和闵氏空间的例子:
\(\mathbb{R}^n\) 上定义度规场 \(\delta\) : \[\delta := \delta_{\mu\nu}\mathrm dx^\mu \otimes dx^\nu\] 则 \((\mathbb{R}^n,\delta)\) 称为n维欧氏空间, \(\delta\) 为欧氏度规
\(ds^2 = \delta_{\mu\nu} \mathrm dx^\mu \mathrm dx^\nu\) 自然坐标基底用欧式度规衡量是正交归一的,因为由 \[\delta({\partial \over\partial x^\alpha } ,{\partial \over\partial x^\beta } ) = \delta_{\mu\nu}\mathrm dx^\mu\otimes \mathrm dx^\nu ({\partial \over\partial x^\alpha},{\partial \over\partial x^\beta } )= \delta_{\mu\nu}\mathrm dx^\mu({\partial \over\partial x^\alpha } )\mathrm dx^\nu({\partial \over\partial x^\beta } )\] 易见 \[\delta({\partial \over\partial x^\alpha } ,{\partial \over\partial x^\beta } )=\delta_{\alpha\beta}\] 但满足欧式度规 \(\delta\) 的未必是自然坐标系。例如,对二维欧式空间,可以对坐标系 \(\{x,y\}\) 作平移和旋转,得到的度规相同。
n维欧氏空间中满足 \(\delta({\partial \over\partial x^\alpha } ,{\partial \over\partial x^\beta } )=\delta_{\alpha\beta}\) 的坐标系为笛卡尔坐标系,或直角坐标系
欧氏空间中的极坐标系:物理上常用基底 \(\{\hat{e_r},\hat{e_\varphi}\}\) 是正交归一的,但非极坐标系基底 \(\{{\partial \over\partial r} ,{\partial \over\partial \varphi } \}\)
\(\displaystyle{\partial \over\partial \varphi }\) 不归一: \[\delta({{\partial \over\partial \varphi } ,{\partial \over\partial \varphi } })=r^2\ne 1\]
度规张量场 \(\iota\) 为: \[\eta := \eta_{\mu\nu} \mathrm dx^\mu \mathrm dx^\nu \\ \eta_{\mu\nu} \equiv \begin{cases} 0, & \mu\ne\nu \\ -1, & \mu = \nu =0 \\ 1,&\mu=\nu = 1,\cdots,n-1 \end{cases}\]
满足该度规的坐标系之间可以通过平移+洛伦兹变换(boost+reflection)相互转化
2.6 抽象指标记号 #
-
\((k,l)\) 型张量用k个上标和l个下标的字母表示,上下指标为小写拉丁字母,只表示张量类型,为抽象指标。例: \(v^a\) 表示矢量 \(\vec v\)
-
重复上下指标表示缩并: \[T^a{}_a = T(e^{\mu*};e_\mu) = T^\mu_\mu\\ T^{ab}{}_a =T(e^{\mu *},\cdot;e_\mu),\\ T^{ab}{}_b =T(\cdot,e^{\mu *};e_\mu )\]
-
张量积记号省略。e.g.: \(T\in\mathscr T_V(2,1),S\in\mathscr T_V(1,1)\) , \(T\otimes S = T^{ab}{}_c S^d{}_e\)
-
涉及张量分量时,使用小写希腊字母。这种指标称为具体指标,可以问及具体数值。 \(T^{\mu\nu}{}_\sigma e_\mu\otimes e_\nu \otimes e^{\sigma*}\) 记成: \[T^{ab}{}_c = T^{\mu\nu}{}_{\sigma} = (e_\mu)^a(e_\nu )^b (e^\sigma)_c\] \((e^\sigma)_c\) 的下标c已经表明是对偶基矢,无需写成 \((e^{\sigma *})_c\)
-
恒等映射 \(\delta^b {}_a\) \(\forall v^a\in V,\delta^a{}_b v^b = v^a\) , \(\forall \omega_a\in V^*,\delta^a{}_b\omega_a = \omega_b\)
-
恒等映射可以用一组基底 \(\{(e_\mu)^a\}\) 和它的对偶基底 \(\{(e^\mu)_a\}\) 表示: \[(e^\mu)_a (e_\mu)^b = \delta^b{}_a\] 度规 \(g\in \mathscr T_V(0,2)\) ,故记作 \(g_{ab}\) , \(g\) 也可看作 \(g:V\to V^*\) 。在度规存在时, \(V\) 与 \(V^*\) 自然在同构映射 \(g\) 下自然认同,而 \(g_{ab}v^b\) 是 \(v^a\) 在这一映射下的像,故应与 \(v^a\) 认同,故将其记作 \(v_a\) ,即 \(g(\cdot,v) = g_{ab}v^b:=v_a\) 。 \(v^a\) 与 \(v_a\) 是两种不同性质的量,但在应用上二者代表同一事物。 度规 \(g\) 是同构映射,它的逆映射 \(g^{-1}:V^*\to V\) 自然存在。不难论证 \(g^{-1}\in \mathscr T_V(2,0)\) ,本应记作 \((g^{-1})^{ab}\) ,但通常记作 \(g^{ab}\) . \(g^{ab}\omega_b\) 记作 \(\omega^a\) ,和 \(\omega_b\) 代表同一事物。 \[\omega^a = g^{ab}\omega_b = g^{ab}(g_{bc}\omega^c) \\ g^{ab}g_{bc}=\delta^a_c\] 这是逆映射的必然结果。 于是,我们可以用度规对张量分量的指标作下降和上升处理。
\(T\in \mathscr T_V(0,2)\) ,为对称的,若 \(T(u,v)=T(v,u)\) 。
对更高阶的张量(如0,l型),定义对称、反对称部分如下:
对称部分: \(T_{(a_1\cdots a_l)}=\frac 1 {l!}\sum_{\pi }^{} T_{a_{\pi(1)\cdots\pi(l)}}\) 反对称部分: \(T_{[a_1\cdots a_l]} = \frac 1 {l!}\sum_\pi \delta_\pi T_{a_{\pi(1)}\cdots a_{\pi(l)}}\) \(\pi\) 为l个数的排列, \(\pi(i)\) 代表排列中第i个数字。 \(\delta_\pi = \pm 1\) (奇排列为-1,偶排列为1)
\(T_{a_1\cdots a_l}=T_{(a_1\cdots a_l)}\) 为全对称张量 \(T_{a_1\cdots a_l }= T_{[a_1\cdots a_l]}\) 为全反对称张量
对于全对称张量, \(T_{a_1\cdots a_l}=T_{a_{\pi(1)}\cdots a_{\pi(l)}}\) ,对任意排列 \(\pi\) 成立 对于全反对称张量, \(T_{a_1\cdots a_l}=\delta_\pi T_{a_{\pi(1)}\cdots a_{\pi(l)}}\) ,对任意排列 \(\pi\) 成立
- 缩并时括号有“传染性”: \[T_{[a_1\cdots a_l]}S^{a_1\cdots a_l} = T_{[a_1\cdots a_l]}S^{[a_1\cdots a_l]} = T_{a_1\cdots a_l} S^{[a_1\cdots a_l]}\]
- 括号内同种子括号可随意增删:
- 括号内加异种子括号得0:
\[T_{[(ab)c]}=0,\qquad T_{(a[bcd])}=0\] 4. 异种括号缩并得0:
\[T^{(abc)}S_{[abc]}=0\] 5. \[T_{a_1\cdots a_l} = T_{(a_1\cdots a_l)}\Rightarrow T_{[a_1\cdots a_l]}=0 \\ T_{a_1\cdots a_l} = T_{[a_1\cdots a_l]}\Rightarrow T_{(a_1\cdots a_l)}=0\]